题目内容
函数 =
= (
( 为常数),若f(x)在(0,+∞)上有最大值10,则
为常数),若f(x)在(0,+∞)上有最大值10,则 在
在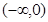 上有( )
上有( )
| A.最大值10 | B.最小值-5 | C.最小值-4 | D.最大值9 |
C
解析考点:三角函数的最值;奇偶性与单调性的综合.
专题:计算题.
分析:函数变形为g(x)=f(x)-3,判断函数g(x)的奇偶性,利用f(x)在(0,+∞)上有最大值10,求出f(x)在(-∞,0)上有最小值,即可.
解答:解:函数f(x)= (a,b为常数),
(a,b为常数),
化为g(x)=f(x)-3=
因为g(-x)= =-[
=-[ ]=-g(x),
]=-g(x),
所以函数g(x)是奇函数,f(x)在(0,+∞)上有最大值10,所以g(x)在(0,+∞)上有最大值7,
g(x)在(-∞,0)上有最小值-7,所以f(x)在(-∞,0)上有最小值-7+3=-4.
故选C.
点评:本题是中档题,考查函数的奇偶性,构造法的应用,整体代入的思想,考查计算能力.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
 (
( 为常数)是奇函数,则实数
为常数)是奇函数,则实数 为( )
为( ) C.
3
D.
C.
3
D. 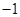
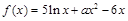 (
(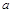 为常数),且
为常数),且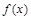 在点
在点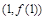 处的切线平行于
处的切线平行于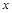 轴.
轴.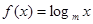 (
(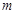 为常数,
为常数,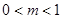 ),且数列
),且数列 是首项为
是首项为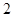 ,公差为
,公差为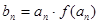 ,当
,当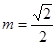 时,求数列
时,求数列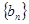 的前
的前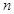 项和
项和 ;
;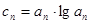 ,如果
,如果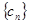 中的每一项恒小于它后面的项,求
中的每一项恒小于它后面的项,求