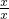Question

下列函数与y=x表示同一函数的是（　　）

• A．y=(

  x

  )2
• B．y=

  3	x3

• C．y=alogax(a＞0且a≠1)
• D．y=

  x2

  x

Answer 1

分析：确定函数的三要素是：定义域、对应法则和值域，若两个函数表示同一函数则要求函数的定义域和解析式必须一致，据此可判断出答案．

解答：解：A中，函数y=(

x

)2=x的定义域为[0，+∞）与y=x的定义域不一致，故不满足条件；
B中，函数y=

3	x3

=x的定义域为R与y=x的定义域一致，故满足条件；
C中，函数y=alogax=x的定义域为（0，+∞）与y=x的定义域不一致，故不满足条件；
D中，函数y=

x2

x

=x的定义域为（-∞，0）∪（0，+∞）与y=x的定义域不一致，故不满足条件；
故选B

点评：本题考查了两函数为同一函数的判断方法，属基础题．当两函数定义域、解析式相同时，值域必相同．