题目内容
数列{an}的通项公式an=
,若{an}的前n项和为24,则n为( )
| 1 | ||||
|
| A、25 | B、576 |
| C、624 | D、625 |
考点:数列的求和
专题:等差数列与等比数列
分析:数列{an}的通项公式an=
=
-
,由此利用裂项求和法求出Sn=
-1由此能求出结果.
| 1 | ||||
|
| n+1 |
| n |
| n+1 |
解答:
解:数列{an}的通项公式an=
=
-
,
∴Sn=
-1+
-
+…+
-
=
-1
∵前n项和为24,∴
-1=24,
解得n=624.
故选:C.
| 1 | ||||
|
| n+1 |
| n |
∴Sn=
| 2 |
| 3 |
| 2 |
| n+1 |
| n |
| n+1 |
∵前n项和为24,∴
| n+1 |
解得n=624.
故选:C.
点评:本题考查数列的项数的求法,解题时要注意裂项求和法的合理运用.基本知识的考查.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
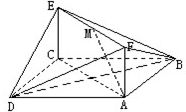 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=