题目内容
不等式|2x-1-log3(x-1)|<|2x-1|+|log3(x-1)|的解集是
(2,+∞)
(2,+∞)
.分析:由|2x-1-log3(x-1)|<|2x-1|+|log3(x-1)|⇒2x-1与log3(x-1)同号且为正,从而可求得其解集.
解答:解:∵|2x-1-log3(x-1)|<|2x-1|+|log3(x-1)|?|(2x-1)-log3(x-1)|2<(2x-1)2+log32(x-1)+2(2x-1)•log3(x-1)⇒4(2x-1)•log3(x-1)>0,
∴
,解得x>2;或
,x∈∅,
∴不等式|2x-1-log3(x-1)|<|2x-1|+|log3(x-1)|的解集是(2,+∞).
故答案为:(2,+∞).
∴
|
|
∴不等式|2x-1-log3(x-1)|<|2x-1|+|log3(x-1)|的解集是(2,+∞).
故答案为:(2,+∞).
点评:本题考查绝对值不等式,关键在于分析出2x-1与log3(x-1)同正,也是难点所在,属于中档题.

练习册系列答案
相关题目
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)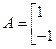
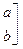 ,A的一个特征值
,A的一个特征值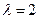 ,其对应的特征向量是
,其对应的特征向量是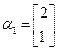 .
.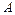 ;
; 在矩阵M所对应的线性变换下的像的方程
在矩阵M所对应的线性变换下的像的方程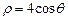 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: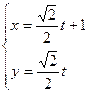 ,
, 求直线l与曲线C相交所成的弦的弦长.
求直线l与曲线C相交所成的弦的弦长.