题目内容
已知函数 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为 .
.(1)求ω值;
(2)求函数y=f(x)的单调递减区间;
(3)已知f(x)在区间
 上的最小值为1,求a的值.
上的最小值为1,求a的值.
【答案】分析:(1)利用二倍角公式、两角和的正弦函数化简函数为 一个角的一个三角函数的形式,通过求出函数的周期求ω值;
(2)利用正弦函数的单调减区间求函数y=f(x)的单调递减区间;
(3)结合 ,求出
,求出 ,求出函数的最小值为1,求出a的值.
,求出函数的最小值为1,求出a的值.
解答:解:(1) (3分)
(3分)
∵ ,∴
,∴ ,∴ω=1(5分)
,∴ω=1(5分)
(2)∵
∴ ,
,
∴单调减区间为 (8分)
(8分)
(3)∵ ,∴
,∴ ,
,
∴ ,
,
∴ ,∴a=1(12分)
,∴a=1(12分)
点评:本题是基础题,考查三角函数的公式的应用,函数的基本性质的灵活运应,考查计算能力,转化思想的应用.
(2)利用正弦函数的单调减区间求函数y=f(x)的单调递减区间;
(3)结合
 ,求出
,求出 ,求出函数的最小值为1,求出a的值.
,求出函数的最小值为1,求出a的值.解答:解:(1)
 (3分)
(3分)∵
 ,∴
,∴ ,∴ω=1(5分)
,∴ω=1(5分)(2)∵

∴
 ,
,∴单调减区间为
 (8分)
(8分)(3)∵
 ,∴
,∴ ,
,∴
 ,
,∴
 ,∴a=1(12分)
,∴a=1(12分)点评:本题是基础题,考查三角函数的公式的应用,函数的基本性质的灵活运应,考查计算能力,转化思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为 .
. 的值;
的值; 中,
中, 分别是角
分别是角 的对边,若
的对边,若
 求
求 的最大值.
的最大值.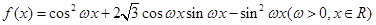 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为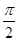 .
.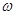 的值;
的值;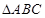 中,
中,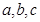 分别是角
分别是角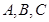 的对边,若
的对边,若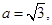
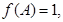 求
求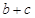 的最大值.
的最大值. 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为 .
. 上的最小值为1,求a的值.
上的最小值为1,求a的值. 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为 ,f(A)=1,求b+c的最大值.
,f(A)=1,求b+c的最大值.