题目内容
已知函数 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为 .
.
(Ⅰ)求ω的值;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,若 ,f(A)=1,求b+c的最大值.
,f(A)=1,求b+c的最大值.
解:(Ⅰ) =
= .(4分)
.(4分)
∵f(x)图象的两条相邻对称轴间的距离为 ,
,
∴f(x)的最小正周期T=π.∴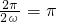 .∴ω=1.(7分)
.∴ω=1.(7分)
(Ⅱ)由 ,得
,得 .
.
∵0<A<π,∴ .∴
.∴ .∴
.∴ .(11分)
.(11分)
由余弦定理,得a2=b2+c2-2bccosA,
因此, .∴(b+c)2≤12.
.∴(b+c)2≤12.
于是,当b=c即△ABC为正三角形时,b+c的最大值为 .(14分)
.(14分)
分析:(Ⅰ)利用二倍角公式、两角和的正弦函数化简函数为一个角的一个三角函数的形式,根据题意求出周期,然后求ω的值;
(Ⅱ)通过f(A)=1,求出A的值,利用余弦定理关于b+c的表达式,然后求其最大值.
点评:本题是基础题,考查三角函数的化简求值,解三角形的知识,二倍角公式、两角和的正弦函数、余弦定理的应用,考查计算能力,注意A的大小求解,是易错点.
 =
= .(4分)
.(4分)∵f(x)图象的两条相邻对称轴间的距离为
 ,
,∴f(x)的最小正周期T=π.∴
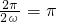 .∴ω=1.(7分)
.∴ω=1.(7分)(Ⅱ)由
 ,得
,得 .
.∵0<A<π,∴
 .∴
.∴ .∴
.∴ .(11分)
.(11分)由余弦定理,得a2=b2+c2-2bccosA,
因此,
 .∴(b+c)2≤12.
.∴(b+c)2≤12.于是,当b=c即△ABC为正三角形时,b+c的最大值为
 .(14分)
.(14分)分析:(Ⅰ)利用二倍角公式、两角和的正弦函数化简函数为一个角的一个三角函数的形式,根据题意求出周期,然后求ω的值;
(Ⅱ)通过f(A)=1,求出A的值,利用余弦定理关于b+c的表达式,然后求其最大值.
点评:本题是基础题,考查三角函数的化简求值,解三角形的知识,二倍角公式、两角和的正弦函数、余弦定理的应用,考查计算能力,注意A的大小求解,是易错点.

练习册系列答案
相关题目
 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为 .
. 的值;
的值; 中,
中, 分别是角
分别是角 的对边,若
的对边,若
 求
求 的最大值.
的最大值.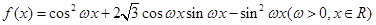 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为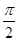 .
.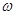 的值;
的值;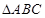 中,
中,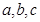 分别是角
分别是角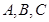 的对边,若
的对边,若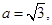
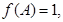 求
求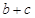 的最大值.
的最大值. 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为 上的最小值为1,求a的值.
上的最小值为1,求a的值. 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为 .
. 上的最小值为1,求a的值.
上的最小值为1,求a的值.