题目内容
【题目】已知函数![]() ,其中
,其中![]() 为常数.
为常数.
(Ⅰ)若![]() 的图像在
的图像在![]() 处的切线经过点(3,4),求
处的切线经过点(3,4),求![]() 的值;
的值;
(Ⅱ)若![]() ,求证:
,求证: 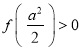 ;
;
(Ⅲ)当函数![]() 存在三个不同的零点时,求
存在三个不同的零点时,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() .
.
【解析】试题分析:(1)根据导数的几何意义可得:![]() ,再结合斜率公式
,再结合斜率公式![]() 进而得出
进而得出![]() 的值;(2)表示出
的值;(2)表示出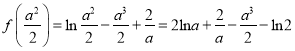 ,然后构造函数
,然后构造函数![]() 通过讨论函数的单调性证明
通过讨论函数的单调性证明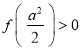 ;(3)将函数零点的问题转化为函数图像与
;(3)将函数零点的问题转化为函数图像与![]() 轴交点个数的问题,通过导数讨论函数的单调性来解决.
轴交点个数的问题,通过导数讨论函数的单调性来解决.
试题解析:由题知![]()
(Ⅰ)![]()
![]() 2分
2分
![]()
![]() 4分
4分
(Ⅱ)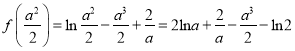 ,令
,令![]() ,
,
则![]() 7分
7分
∴![]() 时,
时, ![]() 单调递减,
单调递减,
故![]() 时,
时, ![]() ,
,
∴当![]() 时,
时,  9分
9分
(Ⅲ)![]()
①![]()
∴![]() 至多只有一个零点,不合题意; 10分
至多只有一个零点,不合题意; 10分
②![]()
∴![]() 至多只有一个零点,不合题意; 11分
至多只有一个零点,不合题意; 11分
③![]()
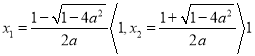
此时, ![]() 在
在![]() 上递减,
上递减, ![]() 上递增,
上递增, ![]() 上递减,所以,
上递减,所以, ![]() 至多有三个零点.因为
至多有三个零点.因为![]() 在
在![]() 递增,所以
递增,所以![]() ,又因为
,又因为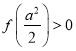 ,所以
,所以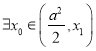 ,使得
,使得![]() ,又
,又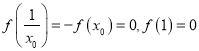 ,所以恰有三个不同零点:
,所以恰有三个不同零点: ![]() ,所以函数
,所以函数![]() 存在三个不同的零点时,
存在三个不同的零点时, ![]() 的取值范围是
的取值范围是![]() . 14分
. 14分

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目