题目内容
给出定义在![]() 上的三个函数:
上的三个函数:
![]() ,
,![]() ,
,![]() .已知
.已知![]() 在
在![]() 处取极值.
处取极值.
(1)确定函数![]() 的单调性;
的单调性;
(2)求证:当![]() 时,恒有
时,恒有![]() 成立;
成立;
(3)把函数![]() 的图象向上平移6个单位得到函数
的图象向上平移6个单位得到函数![]() 的图象,试确定函数
的图象,试确定函数![]() 的
的
零点个数,并说明理由.
【解析】(1)由题设,![]()
由已知,![]() …………………1分
…………………1分
是![]() …………………2分
…………………2分
由![]()
所以![]() 上是增函数,在(0,1)上是减函数. …………………4分
上是增函数,在(0,1)上是减函数. …………………4分
(2)当![]() 时,
时,![]() ,
,
欲证![]() 即证
即证![]() …………………5分
…………………5分
![]()
![]() ……………7分
……………7分![]() 所以
所以![]() 上为增函数.
上为增函数.
从而当![]()
![]() ………………9分
………………9分
(3)由题设,![]() 则
则![]() ………………10分
………………10分
设![]() ,
,![]() ,
,
![]() , ………………12分
, ………………12分
令![]() 得x=1,当
得x=1,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() ,而
,而![]() . ………………13分
. ………………13分
故函数![]() 的图象与x轴有且仅有两个交点,也就是说函数
的图象与x轴有且仅有两个交点,也就是说函数![]() 有两个零点.………14分
有两个零点.………14分

练习册系列答案
相关题目
 则函数
则函数 在(0,1)上有唯一零点;
在(0,1)上有唯一零点; 的定义域中任意的
的定义域中任意的
 必有
必有
 ,则必有
,则必有
 是定义在
是定义在 上的两个函数,对任意
上的两个函数,对任意 满足关系式
满足关系式 但
但 时
时 则函数
则函数 上的三个函数:
上的三个函数: ,已知
,已知 处取极值.
处取极值. 的单调性;
的单调性; 成立.
成立. 的图象,试确定函数
的图象,试确定函数 的零点个数,并说明理由。
的零点个数,并说明理由。 上的三个函数:
上的三个函数: ,已知g(x)在x=1处取极值.
,已知g(x)在x=1处取极值.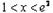 时,恒有
时,恒有 成立;
成立;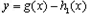 的零点个数,并说明理由。
的零点个数,并说明理由。