题目内容
13.已知数列{an}的首项a1=$\frac{3}{5}$,an+1=$\frac{3{a}_{n}}{2{a}_{n}+1}$,n∈N*.(1)求证:数列{$\frac{1}{{a}_{n}}$-1}为等比数列;
(2)记Sn=$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$,若Sn<100,求满足条件的最大正整数n的值.
分析 (1)利用数列递推式,变形可得得$\frac{1}{{{a_{n+1}}}}-1=\frac{1}{3}({\frac{1}{a_n}-1})$,从而可证数列$\left\{{\frac{1}{a_n}-1}\right\}$为等比数列;
(2)确定数列的通项,利用等比数列的求和公式求和,即可求最大的正整数n.
解答 证明:(1)∵an+1=$\frac{3{a}_{n}}{2{a}_{n}+1}$,
∴$\frac{1}{{a}_{n+1}}$=$\frac{2}{3}$+$\frac{1}{3{a}_{n}}$,
∴$\frac{1}{{{a_{n+1}}}}-1=\frac{1}{3}({\frac{1}{a_n}-1})$,
∵a1=$\frac{3}{5}$,
∴$\frac{1}{{a}_{1}}$-1=$\frac{2}{3}$,
∴$\left\{{\frac{1}{a_n}-1}\right\}$为以$\frac{2}{3}$为首项,以$\frac{1}{3}$为公比的等比数列.
(2)由(1)知$\frac{1}{{a}_{n}}$-1=$\frac{2}{3}$×($\frac{1}{3}$)n-1,
∴$\frac{1}{{a}_{n}}$=2×($\frac{1}{3}$)n+1,
∴Sn=$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$=n+2×($\frac{1}{3}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{3}^{n}}$)=n+2×$\frac{\frac{1}{3}-\frac{1}{{3}^{n+1}}}{1-\frac{1}{3}}$=n+1-$\frac{1}{{3}^{n}}$,
∵Sn<100,
∴${S_n}=n+1-\frac{1}{3^n}<100$,
故nmax=99
点评 本题考查数列递推式,考查等比数列的证明,考查等比数列的求和公式,属于中档题.

| A. | $\frac{3}{4}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
①“若a,b∈R,则a-b=0⇒a=b”类比推出“若a,b∈C,则a-b=0⇒a=b”
②“若a,b,c,d∈R,则复数a+bi=c+di⇒a=c,b=d”
类比推出“若a,b,c,d∈Q,则a+b$\sqrt{2}$=c+d$\sqrt{2}$?a=c,b=d”;
其中类比结论正确的情况是( )
| A. | ①②全错 | B. | ①对②错 | C. | ①错②对 | D. | ①②全对 |
| A. | 18 | B. | $\frac{1}{2}$ | C. | 3 | D. | -9 |
 关于
关于 的方程
的方程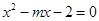 在
在 有解,命题
有解,命题 在
在 单调递增;若
单调递增;若 为真命题,
为真命题, 是真命题,求实数
是真命题,求实数 的取值范围.
的取值范围.