题目内容
设f(x)=|log3x|,若f(x)>f(| 7 | 2 |
分析:由题意f(x)=|log3x|,可以把其代入不等式f(x)>f(
),再去掉绝对值进行求解.
| 7 |
| 2 |
解答:解:∵f(x)=|log3x|,
又∵f(x)>f(
),则|log3x|>|log3
|,
①若x>1,则y=log3x为增函数,∴x>
;
②若0<x<1,则y=log3x为减函数,∴-log3x>log3
,∴0<x<
;
故答案为(0,
)∪(
,+∞).
又∵f(x)>f(
| 7 |
| 2 |
| 7 |
| 2 |
①若x>1,则y=log3x为增函数,∴x>
| 7 |
| 2 |
②若0<x<1,则y=log3x为减函数,∴-log3x>log3
| 7 |
| 2 |
| 2 |
| 7 |
故答案为(0,
| 2 |
| 7 |
| 7 |
| 2 |
点评:此题主要考查对数函数的性质和绝对值的性,考查了分类讨论的思想,是一道中档题.

练习册系列答案
相关题目
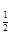 (
(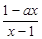 )为奇函数,a为常数.
)为奇函数,a为常数.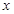 的值,不等式
的值,不等式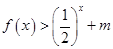 恒成立,求实数
恒成立,求实数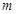 的取值范围.
的取值范围.
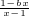 为奇函数,b为常数.
为奇函数,b为常数. )x+m恒成立,求实数m的取值范围.
)x+m恒成立,求实数m的取值范围.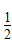
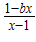 为奇函数,b为常数.
为奇函数,b为常数. )x+m恒成立,求实数m的取值范围.
)x+m恒成立,求实数m的取值范围.