Question

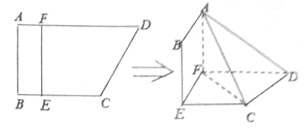
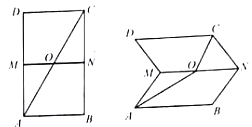
【题目】如图，已知是矩形， ， 分别为边， 的中点， 与交于点，沿将矩形折起，设， ，二面角的大小为.

（1）当时，求的值；

（2）点时，点是线段上一点，直线与平面所成角为.若，求线段的长.

Answer 1

【答案】（1）（2）

【解析】试题解析：（1）当时，根据二面角定义可知：平面平面，于是，可以过点建立空间直角坐标系，然后根据，求出两点坐标，然后根据即可求出结果；（2）时即， 为等边三角形，于是可以求得点，设平面的法向量为，求出法向量的坐标，因为为线段上一点，所以可设，然后可以将点坐标用表示，从而得出的坐标，然后可以与平面的法向量进行运算，得出的值，就可以得到线段的长度.

试题解析：如图，设为的中点，建立如图所示的空间直角坐标系.

（1）当时， ， ，

， ，

.

（2）由得， ， ，

，

设，则，

，

设平面的法向量为， ， ，

，取，

由题意，得，即，

或（舍去），

在线段上存在点，且.