题目内容
在调查男女乘客是否晕机的情况中,已知男乘客晕机为28人,不会晕机的也是28人,而女乘客晕机为28人,不会晕机的为56人,
(1)根据以上数据建立一个![]() 的列联表;
的列联表;
(2)能否在犯错误的概率不超过0.05的前提下认为晕机与性别有关系?
(可能用到的公式:![]() ,可能用到数据:
,可能用到数据:![]() )
)
(1)解:2×2列联表如下: -------------4分
| 晕机 | 不晕机 | 合计 | |
| 男乘客 | 28 | 28 | 56 |
| 女乘客 | 28 | 56 | 84 |
| 合计 | 56 | 84 | 140 |
(2)假设是否晕机与性别无关,则![]() 的观测值
的观测值![]()
-------------8分
![]() ,
,
所以可以在犯错误的概率不超过0.05的前提下认为晕机与性别有关系 ………10分

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
某课外小组在调查男女乘客是否晕机的情况中,获得男乘客晕机为28人,不会晕机的也是28人,而女乘客晕机为28人,不会晕机的为56人,根据列联表的数据,可以有__________的把握认为晕机与性别有关.
数据列联表:
独立性检验临界值表:
|
P(k2≥k0) |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
|
k0 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
|
]
|
|
晕机 |
不晕机 |
合计 |
|
男乘客 |
28 |
28 |
56 |
|
女乘客 |
28 |
56 |
84 |
|
合计 |
56 |
84 |
140 |
独立性检验随机变量K2值的计算公式: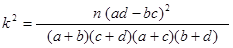
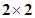 的列联表;(2)能否在犯错误的概率不超过0.05的前提下认为晕机与性别有关?
的列联表;(2)能否在犯错误的概率不超过0.05的前提下认为晕机与性别有关?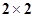 的列联表;
的列联表;