题目内容
设f(x)=x2-2ax+2.当x∈［-1,+∞)时，f(x)≥a恒成立，求实数a的取值范围.解:(1)当a≤-1时，f(x)min=f(-1)=3+2a,x∈［-1,+∞),f(x)≥a恒成立
f(x)min≥a，即3+2a≥a
a≥-3.故此时-3≤a≤-1.
(2)当a＞-1时，f(x)min=f(a)=a2-2a2+2=2-a2,x∈［-1,+∞),f(x)≥a恒成立
f(x)min≥a,即2-a2≥a
a2+a-2≤0
-2≤a≤1.故此时-1＜a≤1.
由(1)(2)知，当-3≤a≤1时，x∈［-1,+∞),f(x)≥a恒成立.
练习册系列答案
相关题目
)
，+∞)
,+∞)
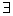x0∈(0，+∞)使得f(x0)≥g(x0)，则实数m的取值范围是
B. 
C. 
D. 