题目内容
南充市某商场在经营某种商品的80天内发现:其销售量和价格均是时间x的函数.其中销售量满足f (x)=-
x+40(0<x≤80,x∈N+),在前40天内价格为g1(x)=
x+10,(0<x≤40,x∈N+),在后40天内价格为g2(x)=-
x+30(40<x≤80,x∈N+).求这种商品哪天的销售额最大,并求最大值.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
分析:先分两段分别写出销售额随时间变化的函数,再利用二次函数配方法分别求两段上的最大值,最后取两段中较大的最大值作为整个函数的最大值即可
解答:解:依题意,商品价格为分段函数g(x)=
,而销售量满足f (x)=-
x+40(0<x≤80,x∈N+),
∴前40天的销售额为y=(
x+10)(-
x+40)=-
(x+40)(x-80)=-
(x-20)2+450≤450,(0<x≤40,x∈N+)(当且仅当x=20时取等号)
后40天的销售额为y=(-
x+30)(-
x+40)=
(x-120)(x-80)=
(x-100)2-50<
(40-100)2-50=400
∴这种商品在第20天销售额最大为450元
|
| 1 |
| 2 |
∴前40天的销售额为y=(
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 8 |
后40天的销售额为y=(-
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
∴这种商品在第20天销售额最大为450元
点评:本题主要考查了将应用问题转化为数学问题的能力,利用二次函数的图象和性质求函数最值的方法,分段函数最值的求法,实现应用问题向数学问题的转化是解决本题的关键

练习册系列答案
相关题目
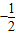 x+40(0<x≤80,x∈N+),在前40天内价格为g1(x)=
x+40(0<x≤80,x∈N+),在前40天内价格为g1(x)=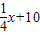 ,(0<x≤40,x∈N+),在后40天内价格为g2(x)=
,(0<x≤40,x∈N+),在后40天内价格为g2(x)=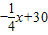 (40<x≤80,x∈N+).求这种商品哪天的销售额最大,并求最大值.
(40<x≤80,x∈N+).求这种商品哪天的销售额最大,并求最大值.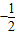 x+40(0<x≤80,x∈N+),在前40天内价格为g1(x)=
x+40(0<x≤80,x∈N+),在前40天内价格为g1(x)=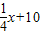 ,(0<x≤40,x∈N+),在后40天内价格为g2(x)=
,(0<x≤40,x∈N+),在后40天内价格为g2(x)=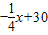 (40<x≤80,x∈N+).求这种商品哪天的销售额最大,并求最大值.
(40<x≤80,x∈N+).求这种商品哪天的销售额最大,并求最大值.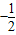 x+40(0<x≤40,x∈N+),在40天内价格为g (x)=
x+40(0<x≤40,x∈N+),在40天内价格为g (x)=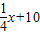 ,(0<x≤40,x∈N+).求这种商品哪天的销售额最大,并求最大值.
,(0<x≤40,x∈N+).求这种商品哪天的销售额最大,并求最大值.