题目内容
已知函数 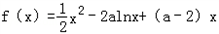 ,a∈R.
,a∈R.
(Ⅰ)当 a=1 时,求函数 f(x) 的最小值;
(Ⅱ)当 a≠0 时,讨论函数 f(x) 的单调性;
(Ⅲ)是否存在实数a,对任意的 x1,x2∈(0,+∞),且x1≠x2,有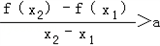 ,恒成立,若存在求出a的取值范围,若不存在,说明理由.
,恒成立,若存在求出a的取值范围,若不存在,说明理由.
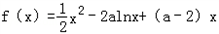 ,a∈R.
,a∈R.(Ⅰ)当 a=1 时,求函数 f(x) 的最小值;
(Ⅱ)当 a≠0 时,讨论函数 f(x) 的单调性;
(Ⅲ)是否存在实数a,对任意的 x1,x2∈(0,+∞),且x1≠x2,有
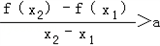 ,恒成立,若存在求出a的取值范围,若不存在,说明理由.
,恒成立,若存在求出a的取值范围,若不存在,说明理由.解:(Ⅰ)由题意,函数f(x)的定义域为(0,+∞),
当a=1 时,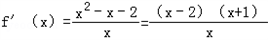
∴当x∈(0,2)时,f′(x)<0,x∈(2,+∞),f'(x)>0.
∴f(x)在x=2时取得极小值且为最小值,其最小值为 f(2)=﹣2ln2
(Ⅱ)∵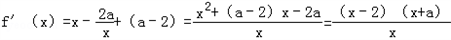 ,
,
∴(1)当﹣2<a≤0时,若x∈(0,﹣a)时,f′(x)>0,f(x)为增函数;
x∈(﹣a,2)时,f′(x)<0,f(x)为减函数;
x∈(2,+∞)时,f′(x)>0,f(x)为增函数.
(2)当a=﹣2时,x∈(0,+∞)时,f(x)为增函数;
(3)当a<﹣2时,x∈(0,2)时,f′(x)>0,f(x)为增函数;
x∈(2,﹣a)时,f′(x)<0,f(x)为减函数;
x∈(﹣a,+∞)时,f′(x)>0,f(x)为增函数
(Ⅲ)假设存在实数a使得对任意的 x1,x2∈(0,+∞),且x1≠x2,
有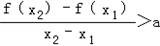 恒成立,
恒成立,
不妨设0<x1<x2,只要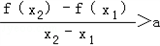 ,
,
即:f(x2)﹣ax2>f(x1)﹣ax1
令g(x)=f(x)﹣ax,只要 g(x)在(0,+∞)为增函数
又函数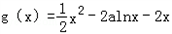 .
.
考查函数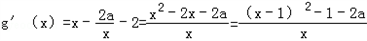
要使g'(x)≥0在(0,+∞)恒成立,
只要﹣1﹣2a≥0,即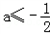 ,
,
故存在实数a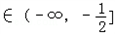 时,
时,
对任意的 x1,x2∈(0,+∞),且x1≠x2,
有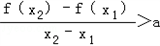 恒成立
恒成立
当a=1 时,
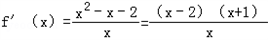
∴当x∈(0,2)时,f′(x)<0,x∈(2,+∞),f'(x)>0.
∴f(x)在x=2时取得极小值且为最小值,其最小值为 f(2)=﹣2ln2
(Ⅱ)∵
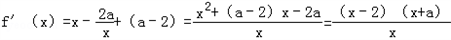 ,
,∴(1)当﹣2<a≤0时,若x∈(0,﹣a)时,f′(x)>0,f(x)为增函数;
x∈(﹣a,2)时,f′(x)<0,f(x)为减函数;
x∈(2,+∞)时,f′(x)>0,f(x)为增函数.
(2)当a=﹣2时,x∈(0,+∞)时,f(x)为增函数;
(3)当a<﹣2时,x∈(0,2)时,f′(x)>0,f(x)为增函数;
x∈(2,﹣a)时,f′(x)<0,f(x)为减函数;
x∈(﹣a,+∞)时,f′(x)>0,f(x)为增函数
(Ⅲ)假设存在实数a使得对任意的 x1,x2∈(0,+∞),且x1≠x2,
有
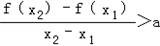 恒成立,
恒成立,不妨设0<x1<x2,只要
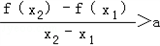 ,
,即:f(x2)﹣ax2>f(x1)﹣ax1
令g(x)=f(x)﹣ax,只要 g(x)在(0,+∞)为增函数
又函数
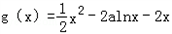 .
.考查函数
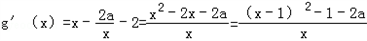
要使g'(x)≥0在(0,+∞)恒成立,
只要﹣1﹣2a≥0,即
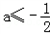 ,
,故存在实数a
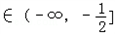 时,
时,对任意的 x1,x2∈(0,+∞),且x1≠x2,
有
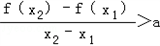 恒成立
恒成立
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (a∈R且a≠0).
(a∈R且a≠0).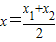 ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. ,a∈R.
,a∈R. 上的任意一个x,都有f(x)≤1成立,求a的取值范围.
上的任意一个x,都有f(x)≤1成立,求a的取值范围. (a∈R).
(a∈R). 在[1,e]上是增函数,求a的取值范围;
在[1,e]上是增函数,求a的取值范围;
 .
.