题目内容

函数y=sin
πx3
在区间[0，n]上至少取得2个最大值，则正整数n的最小值是
 
．
分析：先根据函数的解析式求得函数的最小正周期，进而依据题意可推断出在区间上至少有
5
4
个周期．进而求得n≥6×
5
4
，求得n的最小值．
解答：解：y=sin
πx
3
周期T=
2π
π
3
=6
在区间[0，n]上至少取得2个最大值，说明在区间上至少有
5
4
个周期．
6×
5
4
=
15
2

所以，n≥
15
2

∴正整数n的最小值是8
故答案为8
点评：本题主要考查了三角函数的周期性及其求法．考查了考生对三角函数周期性的理解和灵活利用．
练习册系列答案
相关题目
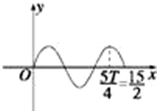精英家教网已知函数y=sin
πx
3
在区间[0，t]上至少取得2次最大值，则正整数t的最小值是（　　）
A、6B、7C、8D、9
下列说法：
①“?x∈R，2x＞3”的否定是“?x∈R，2x≤3”；
②命题“函数y=sin(?x+
π
3
)的最小正周期是π，则?=2”是真命题；
③命题“函数f（x）在x=x0处有极值，则f′（x0）=0”的否命题是假命题；
④f（x）是（-∞，0）∪（0，+∞）上的偶函数，x＞0时f（x）的解析式是f（x）=x3，
则x＜0时f（x）的解析式是f（x）=-x3．
其中正确的说法是（　　）
已知函数y=sin
πx
3
在区间[0，t]上至少取得2次最大值，则正整数t的最小值是（　　）
A．6B．7C．8D．9
精英家教网
函数y=sin
πx
3
在区间[0，n]上至少取得2个最大值，则正整数n的最小值是 ______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网