题目内容
在等边三角形内任取一点,则点M落在其内切圆内部的概率是
- A.
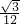
- B.

- C.

- D.

D
分析:求出三角形的面积,再求出内切圆的面积,根据几何概型概率计算公式,求其比值即可解答.
解答: 解:不妨设三角形边长为1,则三角形面积为
解:不妨设三角形边长为1,则三角形面积为 ,
,
内切圆的半径为等边三角形高的三分之一,
即 =
= ,
,
∴内切圆面积为 =
= ,
,
则点M落在其内切圆内部(阴影)区域的概率为 ÷
÷ =
= .
.
故选D.
点评:本题考查几何概率的求法:首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件(A);然后计算阴影区域的面积在总面积中占的比例,这个比例即事件(A)发生的概率.
分析:求出三角形的面积,再求出内切圆的面积,根据几何概型概率计算公式,求其比值即可解答.
解答:
 解:不妨设三角形边长为1,则三角形面积为
解:不妨设三角形边长为1,则三角形面积为 ,
,内切圆的半径为等边三角形高的三分之一,
即
 =
= ,
,∴内切圆面积为
 =
= ,
,则点M落在其内切圆内部(阴影)区域的概率为
 ÷
÷ =
= .
.故选D.
点评:本题考查几何概率的求法:首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件(A);然后计算阴影区域的面积在总面积中占的比例,这个比例即事件(A)发生的概率.

练习册系列答案
相关题目
 B.
B. C.
C. D.
D.
 B.
B. C.
C. D.
D.