题目内容
(2013•湖南模拟)定义在R上的函数f(x)满足f(x+2)=2f(x),当x∈[0,2]时,f(x)=(
-1)(
-4).若f(x)在[-2n,-2n+2](n∈N*)上的最小值为-
,则n( )
| 2 | x |
| 2 | x |
| 9 |
| 32 |
分析:采用换元法并结合二次函数的性质,算出当x∈[0,2]时,[f(x)]min=-
,此时x=log2
.然后类似地算出当x∈[-2,0]、x∈[-4,-2]、x∈[-6,-4]时,f(x)在各个区间上的最小值,即可得到若f(x)在[2n,2n+2]上的最小值为-
时,x∈[-6,-4],由此即可得到本题的答案.
| 9 |
| 4 |
| 5 |
| 2 |
| 9 |
| 32 |
解答:解:①∵当x∈[0,2]时,f(x)=(
-1)(
-4),
∴令2x=t,得f(x)=(t-1)(t-4)=g(t)
当且仅当t=
时,[f(x)]min=g(
)=-
,此时x=log2
∈[0.2].
②当x∈[-2,0]时,f(x)=
f(x+2)=
(
-1)(
-4),
类似①的方法,可得当x=log2
∈[-2,0)时,[f(x)]min=-
;
③当x∈[-4,-2]时,f(x)=
f(x+2)=
(
-1)(
-4)
类似①的方法,可得当x=log2
∈[-4,-2)时,[f(x)]min=-
;
④当x∈[-6,-4]时,f(x)=
f(x+2)=
(
-1)(
-4)
类似①的方法,可得当x=log2
∈[-4,-2)时,[f(x)]min=-
综上所述,若f(x)在[2n,2n+2]上的最小值为-
时,n=3
故选:D
| 2 | x |
| 2 | x |
∴令2x=t,得f(x)=(t-1)(t-4)=g(t)
当且仅当t=
| 5 |
| 2 |
| 5 |
| 2 |
| 9 |
| 4 |
| 5 |
| 2 |
②当x∈[-2,0]时,f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 | x+2 |
| 2 | x+2 |
类似①的方法,可得当x=log2
| 5 |
| 8 |
| 9 |
| 8 |
③当x∈[-4,-2]时,f(x)=
| 1 |
| 2 |
| 1 |
| 4 |
| 2 | x+4 |
| 2 | x+4 |
类似①的方法,可得当x=log2
| 5 |
| 32 |
| 9 |
| 16 |
④当x∈[-6,-4]时,f(x)=
| 1 |
| 2 |
| 1 |
| 8 |
| 2 | x+6 |
| 2 | x+6 |
类似①的方法,可得当x=log2
| 5 |
| 128 |
| 9 |
| 32 |
综上所述,若f(x)在[2n,2n+2]上的最小值为-
| 9 |
| 32 |
故选:D
点评:本题给出抽象函数f(x),在已知在x∈[0,2]时函数表达式且f(x+2)=2f(x)的情况下,求若f(x)在[2n,2n+2]上的最小值为-
时n的值.着重考查了函数的对应法则、二次函数的图象与性质和函数值域求法等知识,属于中档题.
| 9 |
| 32 |

练习册系列答案
相关题目
 (2013•湖南模拟)设椭圆
(2013•湖南模拟)设椭圆 (2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=
(2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=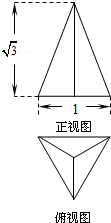 (2013•湖南模拟)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )
(2013•湖南模拟)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( ) (2013•湖南模拟)已知集合M={x∈Z|-1≤x≤1},N={x∈Z|x(x-2)≤0},则如图所示韦恩图中的阴影部分所表示的集合为( )
(2013•湖南模拟)已知集合M={x∈Z|-1≤x≤1},N={x∈Z|x(x-2)≤0},则如图所示韦恩图中的阴影部分所表示的集合为( )