题目内容
(理)若关于x的不等式
lg(1-x2)-lg(ax+b)>0的解集为(-
,
),则满足条件的所有实数对(a,b)共有
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
3
3
对.分析:由关于x的不等式
lg(1-x2)-lg(ax+b)>0的解集为(-
,
),推导出
>1的解集为(-
,
),由此能得到满足条件的所有实数对(a,b)共有3对.
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| ax+b |
| 2 |
| 3 |
| 1 |
| 2 |
解答:解:∵
lg(1-x2)-lg(ax+b)>0,
∴lg
>0,
∴
>1,
∵关于x的不等式
lg(1-x2)-lg(ax+b)>0的解集为(-
,
),
∴
>1的解集为(-
,
),
满足条件的a,b有三种情况:
①x=-
和x=
时,
=1同时存在;
②x=-
时,
=1,x=
时,ax+b=0;
③x=
时,
=1,x=-
时,ax+b=0.
∴
,或
,或
,
∴满足条件的所有实数对(a,b)共有3对.
故答案为:3.
| 1 |
| 2 |
∴lg
| ||
| ax+b |
∴
| ||
| ax+b |
∵关于x的不等式
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
∴
| ||
| ax+b |
| 2 |
| 3 |
| 1 |
| 2 |
满足条件的a,b有三种情况:
①x=-
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| ax+b |
②x=-
| 2 |
| 3 |
| ||
| ax+b |
| 1 |
| 2 |
③x=
| 1 |
| 2 |
| ||
| ax+b |
| 2 |
| 3 |
∴
|
|
|
∴满足条件的所有实数对(a,b)共有3对.
故答案为:3.
点评:本题考查对数不等式的解法和应用,解题时要认真审题,注意对数函数的性质和等价转化思想的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
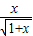 (x>0).
(x>0).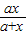 在(0,+∞)上单调递增,求实数a的取值范围.
在(0,+∞)上单调递增,求实数a的取值范围.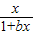
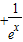 ≥1在[0,+∞)上恒成立,求实数b的最大值.
≥1在[0,+∞)上恒成立,求实数b的最大值.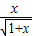 (x>0).
(x>0). 在(0,+∞)上单调递增,求实数a的取值范围.
在(0,+∞)上单调递增,求实数a的取值范围.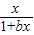
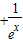 ≥1在[0,+∞)上恒成立,求实数b的最大值.
≥1在[0,+∞)上恒成立,求实数b的最大值. 的解集为
的解集为 ,则满足条件的所有实数对(a,b)共有 对.
,则满足条件的所有实数对(a,b)共有 对.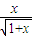 (x>0).
(x>0).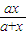 在(0,+∞)上单调递增,求实数a的取值范围.
在(0,+∞)上单调递增,求实数a的取值范围.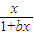
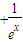 ≥1在[0,+∞)上恒成立,求实数b的最大值.
≥1在[0,+∞)上恒成立,求实数b的最大值.