题目内容
已知函数f（x）=xsinx，x∈R，则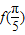
，f（1），
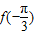的大小关系为（ ）A．
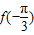
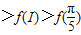
B．
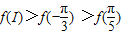
C．
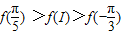
D．
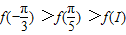
【答案】分析：确定函数为偶函数，x∈（0，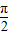
）时，函数是增函数，即可得到结论．
解答：解：∵f（x）=xsinx，
∴f（-x）=（-x）sin（-x）=xsinx=f（x），
∴函数f（x）是偶函数，
∴
=
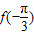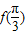
又x∈（0，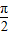
）时，得y′=sinx+xcosx＞0，
∴此时函数是增函数，
∴f（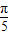
）＜f（1）＜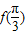
∴
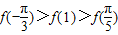
故选A．
点评：本题考查函数的单调性，奇偶性，导数的应用，考查计算能力，是基础题．
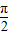）时，函数是增函数，即可得到结论．解答：解：∵f（x）=xsinx，
∴f（-x）=（-x）sin（-x）=xsinx=f（x），
∴函数f（x）是偶函数，
∴
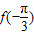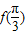
=又x∈（0，
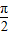）时，得y′=sinx+xcosx＞0，∴此时函数是增函数，
∴f（
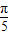）＜f（1）＜∴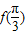
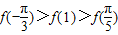
故选A．
点评：本题考查函数的单调性，奇偶性，导数的应用，考查计算能力，是基础题．
练习册系列答案
互动英语系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|