题目内容
《我是歌手》是2013年最受欢迎的歌唱节目之一，它的赛制是：有7位歌手(1至7号)参加一场歌唱比赛, 由500名大众评委现场投票决定歌手名次, 根据年龄将大众评委分为5组, 各组的人数如下:
| 组别 | A | B | C | D | E |
| 人数 | 50 | 100 | 150 | 150 | 50 |
(Ⅰ) 为了调查评委对7位歌手的支持状况, 现用分层抽样方法从各组中抽取若干评委, 其中从B组中抽取了6人. 请将其余各组抽取的人数填入下表.
| 组别 | A | B | C | D | E |
| 人数 | 50 | 100 | 150 | 150 | 50 |
| 抽取人数 | 4 |
(Ⅱ) 在(Ⅰ)中, 若A, B两组被抽到的评委中各有1人支持1号歌手, 现从这两组被抽到的评委中分别任选1人, 求这2人都不支持1号歌手的概率.
（1）
填表如图（每个1分 共4分）
| 组别 | A | B | C | D | E |
| 人数 | 50 | 100 | 150 | 150 | 50 |
| 抽取人数 | 2 | 4 | 6 | 6 | 2 |
（2）设A组的两名评委为A、B，B组的四名评委为a、b、c、d
其中A与a支持1号选手
则从AB两组各取1人的事件包括Aa、Ab、Ac、Ad、Ba、Bb、Bc、Bd
共计8个基本事件…
设“两人都不支持1号选手”的事件为A
则A事件包括Bb、Bc、Bd 共计3个基本事件
所以P(A)=
则这2人都不支持1号歌手的概率为
练习册系列答案
相关题目
下表是某单位在2013年1—5月份用水量（单位：百吨）的一组数据：
|
月份 |
1 |
2 |
3 |
4 |
5 |
|
用水量 |
4 5 |
4 |
3 |
2 5 |
1 8 |
（Ⅰ）若由线性回归方程得到的预测数据与实际检验数据的误差不超过0 05，视为“预测可靠”，通过公式得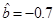
，那么由该单位前4个月的数据中所得到的线性回归方程预测5月份的用水量是否可靠？说明理由；
（Ⅱ）从这5个月中任取2个月的用水量，求所取2个月的用水量之和小于7（单位：百吨）的概率
参考公式：回归直线方程是：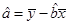
，