题目内容
【题目】已知抛物线![]() 过点
过点![]()
(1)求抛物线![]() 的方程,并求其焦点坐标与准线方程;
的方程,并求其焦点坐标与准线方程;
(2)直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,
,![]() 过点
过点![]() 作
作![]() 轴的垂线分别与直线
轴的垂线分别与直线![]() ,
,![]() 交于
交于![]() ,
,![]() 两点,其中
两点,其中![]() 为坐标原点.若
为坐标原点.若![]() 为线段
为线段![]() 的中点,求证:直线
的中点,求证:直线![]() 恒过定点.
恒过定点.
【答案】(1)抛物线![]() 的方程为
的方程为![]() ,其焦点坐标为
,其焦点坐标为![]() ,准线方程为
,准线方程为![]() (2)证明见解析;
(2)证明见解析;
【解析】
(1) 点![]() 代入求得
代入求得![]() ,即可的抛物线方程求得结果.
,即可的抛物线方程求得结果.
(2) 由题意知直线![]() 斜率存在且不为零,设直线
斜率存在且不为零,设直线![]() 方程为
方程为![]() ,与抛物线方程联立,设
,与抛物线方程联立,设![]() ,
,![]() ,根据已知由
,根据已知由![]() :
:![]() ,
, ![]() :
:![]() ,及过点
,及过点![]() 作
作![]() 轴的垂线求得
轴的垂线求得![]() 的坐标,根据
的坐标,根据![]() 为线段
为线段![]() 的中点,借助韦达定理化简即可证得结论.
的中点,借助韦达定理化简即可证得结论.
解:(1)由抛物线![]() 过点
过点![]() ,
,
得![]() ,所以抛物线
,所以抛物线![]() 的方程为
的方程为![]() ,
,
其焦点坐标为![]() ,准线方程为
,准线方程为![]() .
.
(2)由题意知直线![]() 斜率存在且不为零,设直线
斜率存在且不为零,设直线![]() 方程为
方程为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 的交点为
的交点为![]() ,
,![]() .
.
由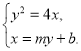 得
得![]() ,
,
由韦达定理,得![]() ,
,![]() .
.
由已知得直线![]() 的方程为
的方程为![]() ,所以
,所以![]() ,
,
由已知得直线![]() 方程为
方程为![]() ,所以
,所以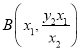 .
.
因为![]() 是线段
是线段![]() 的中点,所以
的中点,所以![]() ①,
①,
将![]() ,
,![]() ,代入①式,并化简得
,代入①式,并化简得![]() ,
,
把![]() ,
,![]() 代入②式,化简得
代入②式,化简得![]()
所以直线![]() 的方程为
的方程为![]() ,故直线
,故直线![]() 恒过定点
恒过定点![]() .
.

【题目】随着生活水平的逐步提高,人们对文娱活动的需求与日俱增,其中观看电视就是一种老少皆宜的娱乐活动.但是我们在观看电视娱乐身心的同时,也要注意把握好观看时间,近期研究显示,一项久坐的生活指标——看电视时间,是导致视力下降的重要因素,即看电视时间越长,视力下降的风险越大.研究者在某小区统计了每天看电视时间![]() (单位:小时)与视力下降人数
(单位:小时)与视力下降人数![]() 的相关数据如下:
的相关数据如下:
编号 | 1 | 2 | 3 | 4 | 5 |
| 1 | 1.5 | 2 | 2.5 | 3 |
| 12 | 16 | 22 | 24 | 26 |
(1)请根据上面的数据求![]() 关于
关于![]() 的线性回归方程
的线性回归方程
(2)我们用(1)问求出的线性回归方程![]() 的
的![]() 估计回归方程
估计回归方程![]() ,由于随机误差
,由于随机误差![]() ,所以
,所以![]() 是
是![]() 的估计值,
的估计值,![]() 成为点(
成为点(![]() ,
,![]() )的残差.
)的残差.
①填写下面的残差表,并绘制残差图;
编号 | 1 | 2 | 3 | 4 | 5 |
| 1 | 1.5 | 2 | 2.5 | 3 |
| 12 | 16 | 22 | 24 | 26 |
|
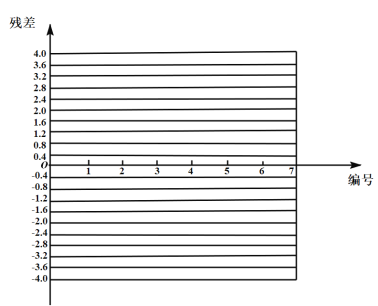
②若残差图所在带状区域宽度不超过4,我们则认为该模型拟合精度比较高,回归方程的预报精度较高,试根据①绘制的残差图分折该模型拟合精度是否比较高?
附:回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为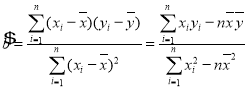 ,
,![]() .
.