题目内容
20.在△ABC中,已知cos2B+cos2C=1+cos2A,且sinA=2sinBcosC,求证:b=c且A=90°.分析 由已知利用三角形内角和定理及两角和与差的正弦函数公式可得sin(B-C)=0,即可解得B=C,可求b=c,利用cos2B=1-sin2B,cos2C=1-sin2C,cos2A=1-sin2A.代入cos2B+cos2C-cos2A=1,可得sin2B+sin2C=sin2A,由正弦定理可得:b2+c2=a2.即可判断A=90°.
解答 证明:∵由 sinA=2sinBcosC,可得:sin(B+C)=2sinBcosC,
即:sinBcosC+cosBsinC=2sinBcosC,
∴sin(B-C)=0,
∴B=C,
∴b=c,
又∵cos2B=1-sin2B,cos2C=1-sin2C,cos2A=1-sin2A.
又cos2B+cos2C=1+cos2A成立,
∴sin2B+sin2C=sin2A,
由正弦定理可得:b2+c2=a2.
∴∠A=90°.
得证.
点评 本题主要考查了三角形内角和定理及两角和与差的正弦函数公式,正弦定理,勾股定理,正弦函数的图象和性质在解三角形中的综合应用,考查了转化思想,属于中档题.

练习册系列答案
相关题目
 已知平行四边形ABCD中,∠A=45°,且AB=BD=1,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图所示:
已知平行四边形ABCD中,∠A=45°,且AB=BD=1,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图所示: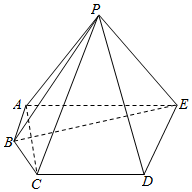 在五棱锥P-ABCDE中,平面PAE⊥平面ABCDE,△PAE为等腰直角三角形,且∠APE=90°,AB=2,AC=$\sqrt{10}$,AE=2AB,BE=2$\sqrt{5}$,DE=3,∠ABC=135°,AB∥DE
在五棱锥P-ABCDE中,平面PAE⊥平面ABCDE,△PAE为等腰直角三角形,且∠APE=90°,AB=2,AC=$\sqrt{10}$,AE=2AB,BE=2$\sqrt{5}$,DE=3,∠ABC=135°,AB∥DE