题目内容

在△ABC中,AB=AC,D、E分别为AB、BC上的点,连结DE并延长交AC的延长线于F.

求证:DECF=EFBD.

图1-3-16

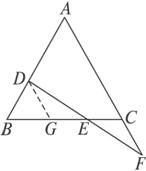
证明:过D作DG∥AC交BC于G，

∴∠BGD=∠ACB.

又∵AB=AC,∴∠B=∠ACB.

∴∠B=∠BGD.

∴BD=DG.

在△DEG和△FEC中,∠EDG=∠F,

∠DEG=∠FEC,

∴△DEG∽△FEC.

∴=.

∴DECF=EFDG.

∴DECF=EFBD.

练习册系列答案
相关题目
如图1，在△ABC中AB⊥AC、AD⊥BC，D是垂足，则AB2=BD•BC（射影定理）．类似的有命题：在三棱锥A-BCD（图2）中，AD⊥平面ABC，AO⊥平面BCD，O为垂足，且O在△BCD内，则（S△ABC）2=S△BCO•S△BCD（S表示面积．上述命题（　　）
已知函数f（x）=2cos2
ωx
2
+sinωx-1（ω＞0）在一个周期内的图象如图所示，且在△ABC中AB=AC=
6

（1）化简该函数表示式，并求出该函数的值域；
（2）求ω的值．
在△ABC中AB=2，C=30°，则
3
BC-AC 的最大值是（　　）
在△ABC中AB=c，AC=b，D为线段BC上一点，且∠BAD=α，∠CAD=β，线段AD=l．
（1）求证：
sinα
b
+
sinβ
c
=
sin(α+β)
l

（2）若AB=4
2
，AC=4，∠BAD=30°，∠CAD=45°，试求线段AD的长．

（本小题满分12分）已知函数．

  （1）设，且，求的值；

  （2）在△ABC中,AB=1,,且△ABC面积为,求sinA+sinB的值．

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网