题目内容

已知函数 $数学公式$
（1）求函数的最小正周期　　　（2）求y取最小值时相应的x值
（3）求函数的单调递增区间　　（4）它的图象可由y=sinx的图象经怎样的变换得出？

解：（1）函数 $\text{[math]}$ 所以函数的周期T= $\text{[math]}$ ；
（2）函数 $\text{[math]}$ 的最小值为： $\text{[math]}$ ；此时 $\text{[math]}$
（3）由 $\text{[math]}$ ，解得函数的单调增区间为： $\text{[math]}$
（4）y=sinx的图象经左移 $\text{[math]}$ ，横坐标不变，横坐标缩短为原来的 $\text{[math]}$ 倍，然后纵坐标缩短为原来的 $\text{[math]}$ 倍，然后上移1单位即可得到函数 $\text{[math]}$ 的图象．
分析：（1）直接利用周期公式求出函数的周期．（2）利用正弦函数的最值求出函数的最小值以及相应的x值．
（3）利用正弦函数的单调增区间求出函数的单调增区间．（4）利用左加右减，上加下减的原则，写出变换过程．
点评：本题是基础题，考查正弦函数的基本性质，周期性、最值、单调增区间、图象的变换，考查计算能力，逻辑推理能力．

练习册系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜

）的图象和y轴交于（0，1）且y轴右侧的第一个最大值、最小值点分别为P（x₀，2）和Q（x₀+3π，-2）．
（1）求函数y=f（x）的解析式及x₀；
（2）求函数y=f（x）的单调递减区间；
（3）如果将y=f（x）图象上所有点的横坐标缩短到原来的

（纵坐标不变），然后再将所得图象沿x轴负方向平移

个单位，最后将y=f（x）图象上所有点的纵坐标缩短到原来的

（横坐标不变）得到函数y=g（x）的图象，写出函数y=g（x）的解析式并给出y=|g（x）|的对称轴方程．

已知函数f（x）=Asin（3x+φ）（ A＞0，x∈（-∞，+∞），0＜φ＜π ）在x=

时取得最大值4．
（1）求函数f（x）的最小正周期及解析式；
（2）求函数f（x）的单调增区间；
（3）求函数f（x）在[0，

]上的值域．

已知函数（1）求函数在区间[1，]上的最大值、最小值；

（2）求证：在区间（1，）上，函数图象在函数图象的下方；

（3）设函数，求证：≥。（）

（1）求函数f（x）的最小正周期和最小值；
（2）在给出的直角坐标系中，用描点法画出函数y=f（x）在区间[0，π]上的图象．

（本题满分12分）

已知函数

（1）求函数的极值点；

（2）若直线过点（0，—1），并且与曲线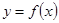相切，求直线的方程；

（3）设函数，其中，求函数在上的最小值.（其中e为自然对数的底数）