题目内容
13. 如图所示的数阵是由非零自然数连续排列构成的,其中第n行中有n个数,则第n行所有数的和是$\frac{1}{2}$n(n2+1).
如图所示的数阵是由非零自然数连续排列构成的,其中第n行中有n个数,则第n行所有数的和是$\frac{1}{2}$n(n2+1).
分析 数阵的第n行有n个数,求得第n行最右边的数为$\frac{1}{2}$n(n+1),则第n行最左边的数为为$\frac{1}{2}$n(n+1)-(n-1),由等差数列的求和公式计算即可得到.
解答 解:数阵的第n行有n个数,前n行所有个数为:1+2+3+…+n=$\frac{1}{2}$n(n+1),
所以,第n行最右边的数为$\frac{1}{2}$n(n+1).
第n行最左边的数为$\frac{1}{2}$n(n+1)-(n-1)=$\frac{1}{2}$n2-$\frac{1}{2}$n+1,
即有第n行所有数的和是$\frac{1}{2}$n($\frac{1}{2}$n2-$\frac{1}{2}$n+1+$\frac{1}{2}$n(n+1))
=$\frac{1}{2}$n(n2+1).
故答案为:$\frac{1}{2}$n(n2+1).
点评 本题考查数列的应用,着重考查等差数列的求和公式的应用,突出考查观察问题、分析问题、解决问题的能力,考查学生数学的思维品质,属于中档题.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
2.已知a+$\frac{1}{a}$=3,则a${\;}^{\frac{1}{2}}$+a${\;}^{-\frac{1}{2}}$等于( )
| A. | 2 | B. | $\sqrt{5}$ | C. | -$\sqrt{5}$ | D. | $±\sqrt{5}$ |
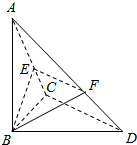 已知△ABC中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别为AC,AD上的动点,且AE:AC=AF:AD=k,k∈(0,1).
已知△ABC中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别为AC,AD上的动点,且AE:AC=AF:AD=k,k∈(0,1).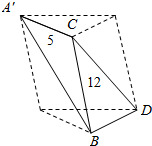 将两直角边长分别为5和12的直角三角板的一条直角边对接成三棱锥A′-BCD,使A′C与BD成60°角,求体积VA′-BCD.
将两直角边长分别为5和12的直角三角板的一条直角边对接成三棱锥A′-BCD,使A′C与BD成60°角,求体积VA′-BCD.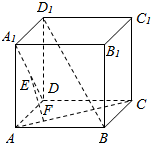 如图,在正方体ABCD-A1B1C1D1中,点E,F分别在A1D,AC上,且EF⊥A1D,EF⊥AC.求证:EF∥BD1.
如图,在正方体ABCD-A1B1C1D1中,点E,F分别在A1D,AC上,且EF⊥A1D,EF⊥AC.求证:EF∥BD1.