题目内容
已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元.设该公司一年内共生产该品牌服装x千件并全部销售完,每千件的销售收入为R(x)万元,且R(x)=
|
(1)写出年利润W(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得利润最大?(注:年利润=年销售收入-年总成本)
分析:(1)由年利润W=年产量x×每千件的销售收入为R(x)-成本,又由R(x)=
,且年固定成本为10万元,每生产1千件需另投入2.7万元.我们易得年利润W(万元)关于年产量x(千件)的函数解析式;
(2)由(1)的解析式,我们求出各段上的最大值,即利润的最大值,然后根据分段函数的最大值是各段上最大值的最大者,即可得到结果.
|
(2)由(1)的解析式,我们求出各段上的最大值,即利润的最大值,然后根据分段函数的最大值是各段上最大值的最大者,即可得到结果.
解答:解:(1)当0<x≤10时,W=xR(x)-(10+2.7x)=8.1x-
-10;
当x>10时,W=xR(x)-(10+2.7x)=98-
-2.7x.
∴W=W=
(2)①当0<x<10时,由W'=8.1-
=0,得x=9,
且当x∈(0,9)时,W'>0;当x∈(9,10)时,W'<0,
∴当x=9时,W取最大值,且Wmax=8.1×9-
×93-10=38.6
②当x>10时,W=98-(
+2.7x)≤98-2
=38
当且仅当
=2.7x,
即x=
时,W=38,
故当x=
时,W取最大值38.
综合①②知当x=9时,W取最大值38.6万元,故当年产量为9千件时,该公司在这一品牌服装的生产中所获年利润最大.
| x3 |
| 30 |
当x>10时,W=xR(x)-(10+2.7x)=98-
| 1000 |
| 3x |
∴W=W=
|
(2)①当0<x<10时,由W'=8.1-
| x2 |
| 10 |
且当x∈(0,9)时,W'>0;当x∈(9,10)时,W'<0,
∴当x=9时,W取最大值,且Wmax=8.1×9-
| 1 |
| 30 |
②当x>10时,W=98-(
| 1000 |
| 3x |
|
当且仅当
| 1000 |
| 3x |
即x=
| 100 |
| 9 |
故当x=
| 100 |
| 9 |
综合①②知当x=9时,W取最大值38.6万元,故当年产量为9千件时,该公司在这一品牌服装的生产中所获年利润最大.
点评:本题考查的知识点是分段函数及函数的最值,分段函数分段处理,这是研究分段函数图象和性质最核心的理念,具体做法是:分段函数的定义域、值域是各段上x、y取值范围的并集,分段函数的奇偶性、单调性要在各段上分别论证;分段函数的最大值,是各段上最大值中的最大者.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
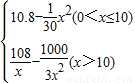
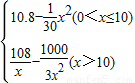
 万元,且R
万元,且R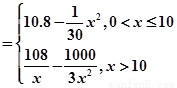 (1)写出年利润
(1)写出年利润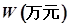 关于年产量
关于年产量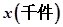 的函数解析式;
的函数解析式;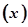 万元,且R
万元,且R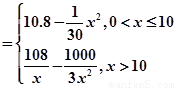
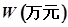 关于年产量
关于年产量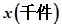 的函数解析式;
的函数解析式;