题目内容
2.已知双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{a}$=1的右焦点的坐标为($\sqrt{13}$,0),则a=4.分析 由题意可得9+a=13,即可得到a的值.
解答 解:双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{a}$=1的右焦点的坐标为($\sqrt{13}$,0),则9+a=13,
所以a=4,
故答案为:4.
点评 本题考查双曲线的方程和性质,考查运算能力,属于基础题.

练习册系列答案
相关题目
17.甲、乙两人在一次设计比赛中各射靶5次,两人成绩的条形图如图所示,则( )
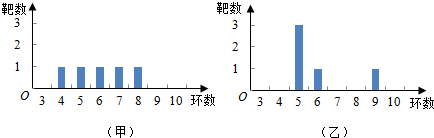

| A. | 甲的成绩的平均数小于乙的成绩的平均数 | |
| B. | 甲的成绩的极差小于乙的成绩的极差 | |
| C. | 甲的成绩的方差小于乙的成绩的方差 | |
| D. | 甲的成绩的中位数等于乙的成绩的中位数 |
11.二次函数f(x)=ax2+bx+c(a>0)的图象与x轴交点的横坐标为-5和3,则这个二次函数的单调减区间为( )
| A. | (-∞,-1] | B. | [2,+∞) | C. | (-∞,2] | D. | [-1,+∞) |