题目内容
已知θ为第二象限角,sin(π-θ)= ,cos
,cos 的值为
的值为
- A.

- B.

- C.±

- D.±

C
分析:根据诱导公式求出sinθ 的值,由同角三角函数的基本关系求出cosθ=- .再判断
.再判断 的范围,由 cosθ=-
的范围,由 cosθ=- =
=
2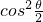 -1,解方程求得 cos
-1,解方程求得 cos 的值.
的值.
解答:已知θ为第二象限角,sin(π-θ)=
∴sinθ= ,cosθ=-
,cosθ=- .
.
由2kπ+ <θ<2kπ+π,k∈z,可得 kπ+
<θ<2kπ+π,k∈z,可得 kπ+ <
< <kπ+
<kπ+ k∈z,
k∈z,
故 是第一或第三象限角.
是第一或第三象限角.
由 cosθ=- =2
=2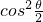 -1,解得 cos
-1,解得 cos =±
=± ,
,
故选C.
点评:本题主要考查同角三角函数的基本关系式,诱导公式,根据角的范围求得对应的三角函数的取值范围,二倍角公式
的应用,考查计算能力,是基础题.
分析:根据诱导公式求出sinθ 的值,由同角三角函数的基本关系求出cosθ=-
 .再判断
.再判断 的范围,由 cosθ=-
的范围,由 cosθ=- =
=2
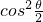 -1,解方程求得 cos
-1,解方程求得 cos 的值.
的值.解答:已知θ为第二象限角,sin(π-θ)=

∴sinθ=
 ,cosθ=-
,cosθ=- .
.由2kπ+
 <θ<2kπ+π,k∈z,可得 kπ+
<θ<2kπ+π,k∈z,可得 kπ+ <
< <kπ+
<kπ+ k∈z,
k∈z,故
 是第一或第三象限角.
是第一或第三象限角.由 cosθ=-
 =2
=2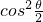 -1,解得 cos
-1,解得 cos =±
=± ,
,故选C.
点评:本题主要考查同角三角函数的基本关系式,诱导公式,根据角的范围求得对应的三角函数的取值范围,二倍角公式
的应用,考查计算能力,是基础题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 ,则2a是( )
,则2a是( ) ,
, 为第二象限角,求
为第二象限角,求 ;
; ,求
,求 的值。
的值。 ,
, 为第二象限角,求
为第二象限角,求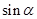 和
和 及
及 的值.
的值.