题目内容
过椭圆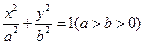 的左焦点
的左焦点 任作一条与两坐标轴都不垂直的弦
任作一条与两坐标轴都不垂直的弦 ,若点
,若点 在
在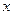 轴上,且使得
轴上,且使得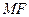 为
为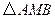 的一条内角平分线,则称点
的一条内角平分线,则称点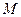 为该椭圆的“左特征点”.
为该椭圆的“左特征点”.
(1)求椭圆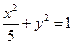 的“左特征点”
的“左特征点” 的坐标;
的坐标;
(2)试根据(1)中的结论猜测:椭圆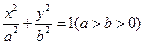 的“左特征点”
的“左特征点” 是一个怎样的点?
是一个怎样的点?
并证明你的结论.
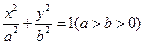 的左焦点
的左焦点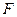 任作一条与两坐标轴都不垂直的弦
任作一条与两坐标轴都不垂直的弦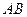 ,若点
,若点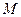 在
在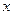 轴上,且使得
轴上,且使得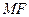 为
为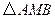 的一条内角平分线,则称点
的一条内角平分线,则称点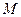 为该椭圆的“左特征点”.
为该椭圆的“左特征点”.(1)求椭圆
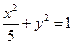 的“左特征点”
的“左特征点”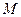 的坐标;
的坐标;(2)试根据(1)中的结论猜测:椭圆
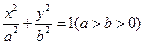 的“左特征点”
的“左特征点”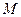 是一个怎样的点?
是一个怎样的点?并证明你的结论.
(1) (2)证明略
(2)证明略
 (2)证明略
(2)证明略(1) ;(2)
;(2)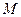 为椭圆的“左特征点”,证明略.
为椭圆的“左特征点”,证明略.
 ;(2)
;(2)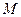 为椭圆的“左特征点”,证明略.
为椭圆的“左特征点”,证明略.
练习册系列答案
相关题目
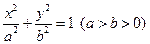 , 线段
, 线段 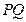 是过左焦点
是过左焦点 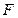 且不与
且不与 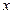 轴垂直的焦点弦. 若在左准线上存在点
轴垂直的焦点弦. 若在左准线上存在点 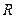 , 使
, 使 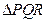 为正三角形, 求椭圆的离心率
为正三角形, 求椭圆的离心率 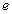 的取值范围, 并用
的取值范围, 并用  为椭圆
为椭圆 的左焦点,点
的左焦点,点 ,动点
,动点 在椭圆上,则
在椭圆上,则 的最小值为
的最小值为 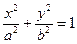 (a>b>0)的一个焦点且垂直于x轴的直线与椭圆C交于点(
(a>b>0)的一个焦点且垂直于x轴的直线与椭圆C交于点(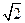 ,1).(1)求椭圆C的方程;(2)设过点P(4,1)的动直线
,1).(1)求椭圆C的方程;(2)设过点P(4,1)的动直线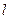 与椭圆C相交于两个不同点A、B,与直线2x+y-2=0交于点Q,若
与椭圆C相交于两个不同点A、B,与直线2x+y-2=0交于点Q,若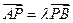 ,
,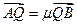 ,求λ+μ的值
,求λ+μ的值 的左右两个焦点,O为坐标原点,点P
的左右两个焦点,O为坐标原点,点P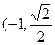 )在椭圆上,线段PB与y轴的交点M为线段PB的中点。
)在椭圆上,线段PB与y轴的交点M为线段PB的中点。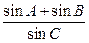 的值。
的值。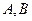 是椭圆
是椭圆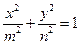 (
( ,
, )上两点,且
)上两点,且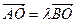 ,则
,则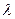 =
=  ,则
,则 与
与 的大小关系为__________________。
的大小关系为__________________。