题目内容
17.已知复数$z=\frac{2i}{1-i}$(i为虚数单位),z的共轭复数为$\overline{z}$,则$z+\overline{z}$=( )| A. | 2i | B. | -2i | C. | -2 | D. | 2 |
分析 利用复数的运算法则、共轭复数的定义即可得出.
解答 解:复数$z=\frac{2i}{1-i}$=$\frac{2i(1+i)}{(1-i)(1+i)}$=i-1,
z的共轭复数为$\overline{z}$=-1-i,
则$z+\overline{z}$=-1+i-1-i=-2.
故选:C.
点评 本题考查了复数的运算法则、共轭复数的定义,考查了计算能力,属于基础题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
5.已知函数f(x)=$\left\{\begin{array}{l}{x+1,0≤x<1}\\{{2}^{x-1}-1,1≤x<3}\end{array}\right.$,若存在m,n,当0≤m<n<3时,有f(m)=f(n),则nf(m)的取值范围是( )
| A. | [1,3) | B. | [1,2log23+2) | C. | [2,3) | D. | [2,2log23+2) |
6.函数f(x)是定义在R上的奇函数,且f(x-1)为偶函数,当x∈[0,1]时,f(x)=x${\;}^{\frac{1}{2}}$,若g(x)=f(x)-2x-b有三个零点,则实数b的取值范围是( )
| A. | (k-$\frac{1}{8}$,k+$\frac{1}{8}$),k∈Z | B. | (2k-$\frac{1}{8}$,2k+$\frac{1}{8}$),k∈Z | C. | (4k-$\frac{1}{8}$,4k+$\frac{1}{8}$),k∈Z | D. | (8k-$\frac{1}{8}$,8k+$\frac{1}{8}$),k∈Z |
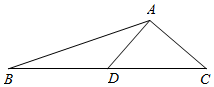 已知如图,△ABC中,AD是BC边的中线,∠BAC=120°,且$\overrightarrow{AB}•\overrightarrow{AC}$=-$\frac{15}{2}$.
已知如图,△ABC中,AD是BC边的中线,∠BAC=120°,且$\overrightarrow{AB}•\overrightarrow{AC}$=-$\frac{15}{2}$.