题目内容
红队队员甲、乙、丙与蓝队队员A、B、C进行围棋比赛,甲对A,乙对B,丙对C各一盘,已知甲胜A,乙胜B,丙胜C的概率分别为0.6,0.5,0.5,假设各盘比赛结果相互独立.(Ⅰ)求红队至少两名队员获胜的概率;
(Ⅱ)用ξ表示红队队员获胜的总盘数,求ξ的分布列和数学期望Eξ.
分析:(I)由题意知红队至少有两名队员获胜包括四种情况,一是只有甲输,二是只有乙输,三是只有丙输,四是三个人都赢,这四种情况是互斥的,根据相互独立事件同时发生的概率和互斥事件的概率得到结果.
(II)由题意知ξ的可能取值是0,1,2,3,结合变量对应的事件写出变量对应的概率,变量等于2使得概率可以用1减去其他的概率得到,写出分布列,算出期望.
(II)由题意知ξ的可能取值是0,1,2,3,结合变量对应的事件写出变量对应的概率,变量等于2使得概率可以用1减去其他的概率得到,写出分布列,算出期望.
解答:解:(I)设甲胜A的事件为D,乙胜B的事件为E,丙胜C的事件为F,
∵甲胜A,乙胜B,丙胜C的概率分别为0.6,0.5,0.5
可以得到D,E,F的对立事件的概率分别为0.4,0,5,0.5
红队至少两名队员获胜包括四种情况:DE
,D
F,
EF,DEF,
这四种情况是互斥的,
∴P=0.6×0.5×0.5+0.6×0.5×0.5+0.4×0.5×0.5+0.6×0.5×0.5=0.55
(II)由题意知ξ的可能取值是0,1,2,3
P(ξ=0)=0.4×0.5×0.5=0.1.,
P(ξ=1)=0.4×0.5×0.5+0.4×0.5×0.5+0.6×0.5×0.5=0.35
P(ξ=3)=0.6×0.5×0.5=0.15
P(ξ=2)=1-0.1-0.35-0.15=0.4
∴ξ的分布列是

∴Eξ=0×0.1+1×0.35+2×0.4+3×0.15=1.6
∵甲胜A,乙胜B,丙胜C的概率分别为0.6,0.5,0.5
可以得到D,E,F的对立事件的概率分别为0.4,0,5,0.5
红队至少两名队员获胜包括四种情况:DE
. |
| F |
. |
| E |
. |
| D |
这四种情况是互斥的,
∴P=0.6×0.5×0.5+0.6×0.5×0.5+0.4×0.5×0.5+0.6×0.5×0.5=0.55
(II)由题意知ξ的可能取值是0,1,2,3
P(ξ=0)=0.4×0.5×0.5=0.1.,
P(ξ=1)=0.4×0.5×0.5+0.4×0.5×0.5+0.6×0.5×0.5=0.35
P(ξ=3)=0.6×0.5×0.5=0.15
P(ξ=2)=1-0.1-0.35-0.15=0.4
∴ξ的分布列是

∴Eξ=0×0.1+1×0.35+2×0.4+3×0.15=1.6
点评:本题考查互斥事件的概率,考查相互独立事件的概率,考查离散型随机变量的分布列和期望,解题时注意对立事件概率的使用,一般遇到从正面解决比较麻烦的,就选择利用对立事件来解决.

练习册系列答案
相关题目
 表示红队队员获胜的总盘数,求
表示红队队员获胜的总盘数,求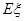 .
. 表示红队队员获胜的总盘数,求
表示红队队员获胜的总盘数,求 。
。