题目内容
红队队员甲、乙、丙与蓝![]() 队队员A、B、C进行围棋比赛,甲对A,乙对B,丙对C各一盘,已知甲胜A,乙胜B,丙胜C的概率分别为0.6,0.5,0.5,假设各盘比赛结果相互独立。
队队员A、B、C进行围棋比赛,甲对A,乙对B,丙对C各一盘,已知甲胜A,乙胜B,丙胜C的概率分别为0.6,0.5,0.5,假设各盘比赛结果相互独立。
(Ⅰ)求红队至少两名队员获胜的概率;
(Ⅱ)用![]() 表示红队队员获胜的总盘
表示红队队员获胜的总盘![]() 数,求
数,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
【解析】(Ⅰ)红队至少两名队员获胜的概率为![]()
![]()
![]() =0.55.
=0.55.
(Ⅱ![]() )
)![]() 取的可能结果为0,1,2,3,则
取的可能结果为0,1,2,3,则
![]()
![]() =0.1;
=0.1;
![]()
![]() +
+![]() +
+![]() =0.35;
=0.35;![]()
![]()
![]()
![]() =0.4;
=0.4;
![]()
![]() =0.15.
=0.15.
所以![]() 的分布列为
的分布列为
|
| 0 | 1 | 2 | 3 |
| P | 0.1 | 0.35 | 0.4 | 0.15 |
数学期望![]() =0×0.1+1×0.35+2×0.4+3×0.15=1.6.
=0×0.1+1×0.35+2×0.4+3×0.15=1.6.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 表示红队队员获胜的总盘数,求
表示红队队员获胜的总盘数,求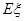 .
. 表示红队队员获胜的总盘数,求
表示红队队员获胜的总盘数,求 。
。