题目内容
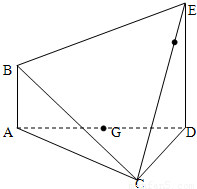
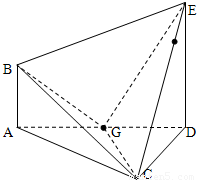
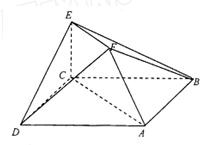
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,G为AD中点.(1)请在线段CE上找到点F的位置,使得恰有直线BF∥平面ACD,并证明这一事实;
(2)求平面BCE与平面ACD所成锐二面角的大小;
(3)求点G到平面BCE的距离.
【答案】分析:解法一:(1)以D点为原点建立如图所示的空间直角坐标系,使得x轴和z轴的正半轴分别经过点A和点E.分别求出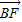 与平面ACD的法向量(可取
与平面ACD的法向量(可取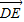 ),只要证明
),只要证明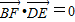 即可.
即可.
(2)分别求平面BCE与平面ACD的法向量的夹角,取其锐角即可.
(3)利用距离公式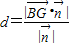 (
(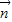 为平面BCE的法向量).
为平面BCE的法向量).
解法二:利用纯几何法解.
(1)分别取CE、CD的中点F、H,连接BF、FH、AH,利用三角形的中位线定理和平行四边形的判定定理及线面平行的判定定理即可证明.
(2)设所求的二面角的大小为θ,则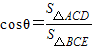 ,利用其公式求出即可.
,利用其公式求出即可.
(3)利用以下转化求出即可VC-BGE=VG-BCE
解答:解法一:以D点为原点建立如图所示的空间直角坐标系,使得x轴和z轴的正半轴分别经过点A和点E,则各点的坐标为D(0,0,0),A(2,0,0),E(0,0,2),B(2,0,1),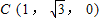 ,
,
(1)点F应是线段CE的中点,下面证明:
设F是线段CE的中点,则点F的坐标为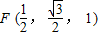 ,∴
,∴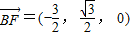 ,取平面ACD的法向量
,取平面ACD的法向量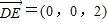 ,
,
则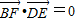 ,
,
∴BF∥平面ACD;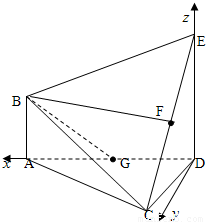
(2)设平面BCE的法向量为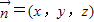 ,
,
则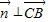 ,且
,且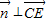 ,
,
由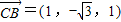 ,
,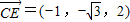 ,
,
∴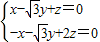 ,不妨设
,不妨设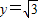 ,则
,则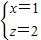 ,即
,即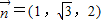 ,
,
∴所求角θ满足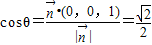 ,∴
,∴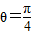 ;
;
(3)由已知G点坐标为(1,0,0),∴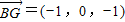 ,
,
由(2)平面BCE的法向量为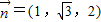 ,
,
∴所求距离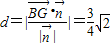 .
.
解法二:(1)由已知AB⊥平面ACD,DE⊥平面ACD,∴AB∥ED,
设F为线段CE的中点,H是线段CD的中点,
连接FH,则FH∥=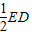 ,∴FH∥=AB,
,∴FH∥=AB,
∴四边形ABFH是平行四边形,∴BF∥AH,
由BF?平面ACD内,AH?平面ACD,∴BF∥平面ACD;
(2)由已知条件可知△ACD即为△BCE在平面ACD上的射影,
设所求的二面角的大小为θ,则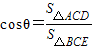 ,
,
易求得BC=BE=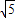 ,CE=
,CE=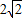 ,
,
∴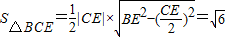 ,
,
而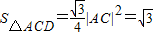 ,
,
∴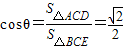 ,而
,而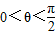 ,
,
∴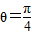 ;
;
(3)连接BG、CG、EG,得三棱锥C-BGE,
由ED⊥平面ACD,∴平面ABED⊥平面ACD,
又CG⊥AD,∴CG⊥平面ABED,
设G点到平面BCE的距离为h,则VC-BGE=VG-BCE即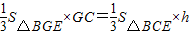 ,
,
由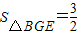 ,
,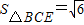 ,
,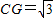 ,
,
∴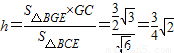 即为点G到平面BCE的距离.
即为点G到平面BCE的距离.
点评:本题综合考查了线面平行、二面角及点到平面的距离,解法一是通过建立空间直角坐标系利用平面的法向量及数量积解决的;解法二是纯几何法,利用三角形的中位线定理、平行四边形的判定定理及线面平行的判定定理,二面角的公式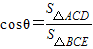 ,及等积转化思想解决的.
,及等积转化思想解决的.
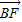 与平面ACD的法向量(可取
与平面ACD的法向量(可取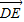 ),只要证明
),只要证明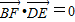 即可.
即可.(2)分别求平面BCE与平面ACD的法向量的夹角,取其锐角即可.
(3)利用距离公式
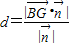 (
(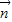 为平面BCE的法向量).
为平面BCE的法向量).解法二:利用纯几何法解.
(1)分别取CE、CD的中点F、H,连接BF、FH、AH,利用三角形的中位线定理和平行四边形的判定定理及线面平行的判定定理即可证明.
(2)设所求的二面角的大小为θ,则
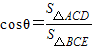 ,利用其公式求出即可.
,利用其公式求出即可.(3)利用以下转化求出即可VC-BGE=VG-BCE
解答:解法一:以D点为原点建立如图所示的空间直角坐标系,使得x轴和z轴的正半轴分别经过点A和点E,则各点的坐标为D(0,0,0),A(2,0,0),E(0,0,2),B(2,0,1),
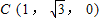 ,
,(1)点F应是线段CE的中点,下面证明:
设F是线段CE的中点,则点F的坐标为
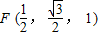 ,∴
,∴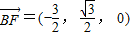 ,取平面ACD的法向量
,取平面ACD的法向量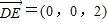 ,
,则
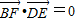 ,
,∴BF∥平面ACD;

(2)设平面BCE的法向量为
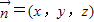 ,
,则
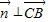 ,且
,且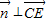 ,
,由
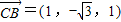 ,
,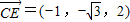 ,
,∴
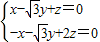 ,不妨设
,不妨设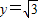 ,则
,则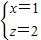 ,即
,即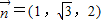 ,
,∴所求角θ满足
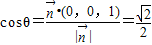 ,∴
,∴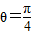 ;
; (3)由已知G点坐标为(1,0,0),∴
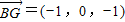 ,
,由(2)平面BCE的法向量为
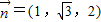 ,
,∴所求距离
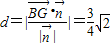 .
. 解法二:(1)由已知AB⊥平面ACD,DE⊥平面ACD,∴AB∥ED,
设F为线段CE的中点,H是线段CD的中点,
连接FH,则FH∥=
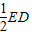 ,∴FH∥=AB,
,∴FH∥=AB,∴四边形ABFH是平行四边形,∴BF∥AH,
由BF?平面ACD内,AH?平面ACD,∴BF∥平面ACD;
(2)由已知条件可知△ACD即为△BCE在平面ACD上的射影,
设所求的二面角的大小为θ,则
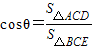 ,
,易求得BC=BE=
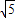 ,CE=
,CE=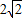 ,
,∴
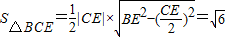 ,
,而
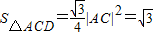 ,
,
∴
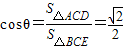 ,而
,而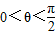 ,
,∴
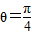 ;
; (3)连接BG、CG、EG,得三棱锥C-BGE,
由ED⊥平面ACD,∴平面ABED⊥平面ACD,
又CG⊥AD,∴CG⊥平面ABED,
设G点到平面BCE的距离为h,则VC-BGE=VG-BCE即
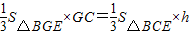 ,
,由
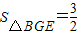 ,
,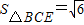 ,
,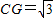 ,
,∴
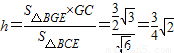 即为点G到平面BCE的距离.
即为点G到平面BCE的距离.点评:本题综合考查了线面平行、二面角及点到平面的距离,解法一是通过建立空间直角坐标系利用平面的法向量及数量积解决的;解法二是纯几何法,利用三角形的中位线定理、平行四边形的判定定理及线面平行的判定定理,二面角的公式
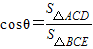 ,及等积转化思想解决的.
,及等积转化思想解决的. 
练习册系列答案
相关题目
 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=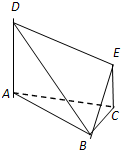 在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1.
在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1. 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,BC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,BC⊥AC,EF∥AC,AB=