题目内容
 如图,四边形OABC是面积为4的正方形,函数y=
如图,四边形OABC是面积为4的正方形,函数y=| k |
| x |
(1)求k的值;
(2)将正方形OABC分别沿直线AB、BC翻折,得到正方形MABC′、NA′BC.设线段MC′、NA′分别与函数y=
| k |
| x |
(3)计算△EOF的面积.
分析:(1)由正方形的面积得到B点的坐标,代入y=
(x>0)求得k的值,则函数解析式可求;
(2)由题意得到E,F的横纵坐标,和(1)中求出的函数联立解得E,F的坐标,由两点式得直线方程;
(3)求出|EF|,利用点到直线的距离公式求出O到直线EF的距离,代入三角形面积公式求解.
| k |
| x |
(2)由题意得到E,F的横纵坐标,和(1)中求出的函数联立解得E,F的坐标,由两点式得直线方程;
(3)求出|EF|,利用点到直线的距离公式求出O到直线EF的距离,代入三角形面积公式求解.
解答:解:(1)由正方形的面积为4得,点B坐标(2,2)
代入函数y=
(x>0),得k=4;
(2)∵正方形MABC′、NA′BC由正方形OABC翻折所得,
∴ON=OM=2OA=4,
∴点E横坐标为4,点F纵坐标为4.
∵点E、F在函数y=
的图象上,
∴当x=4时,y=1,即E(4,1),
当y=4时,x=1,即F(1,4).
设直线EF解析式为y=mx+n,将E、F两点坐标代入,
得m=-1,n=5.
∴直线EF的解析式为y=-x+5.
解析式为y=-x+5;
(3)由E(4,1),F(1,4).
所以|EF|=
=3
.
而O到直线x+y-5=0的距离为d=
=
.
所以△EOF的面积为S=
×3
×
=
.
代入函数y=
| k |
| x |
(2)∵正方形MABC′、NA′BC由正方形OABC翻折所得,
∴ON=OM=2OA=4,
∴点E横坐标为4,点F纵坐标为4.
∵点E、F在函数y=
| 4 |
| x |
∴当x=4时,y=1,即E(4,1),
当y=4时,x=1,即F(1,4).
设直线EF解析式为y=mx+n,将E、F两点坐标代入,
得m=-1,n=5.
∴直线EF的解析式为y=-x+5.
解析式为y=-x+5;
(3)由E(4,1),F(1,4).
所以|EF|=
| (4-1)2+(1-4)2 |
| 2 |
而O到直线x+y-5=0的距离为d=
| |-5| | ||
|
5
| ||
| 2 |
所以△EOF的面积为S=
| 1 |
| 2 |
| 2 |
5
| ||
| 2 |
| 15 |
| 2 |
点评:本题考查了代入法求函数解析式,考查了直线方程的两点式,考查了三角形面积的求法,是中低档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

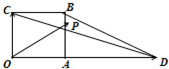 如图,四边形OABC是边长为1的正方形,OD=3,点P为△BCD内(含边界)的动点,设
如图,四边形OABC是边长为1的正方形,OD=3,点P为△BCD内(含边界)的动点,设 (2013•文昌模拟)如图,四边形OABC是边长为1的正方形,OD=3,点P为△BCD内(含边界)的动点,设
(2013•文昌模拟)如图,四边形OABC是边长为1的正方形,OD=3,点P为△BCD内(含边界)的动点,设 如图,四边形OABC是边长为1的正方形,
如图,四边形OABC是边长为1的正方形,