题目内容
10. 如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点,N为AC中点.
如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点,N为AC中点.(Ⅰ)求证:PC⊥AD;
(Ⅱ)在棱PB上是否存在一点Q,使得面MNQ平行面PAD,若存在,指出点Q的位置并证明;若不存在,请说明理由;
(Ⅲ)求点D到平面PAM的距离.
分析 (Ⅰ)先证出线面垂直再证出线线垂直即可;
(Ⅱ)令Q为PB的中点,先证出线面垂直,再证出面面垂直;
(Ⅲ)点D到平面PAM的距离即点D到平面PAC的距离,根据VD-PAC=VP-ACD,求出点D到平面PAM的距离即可.
解答 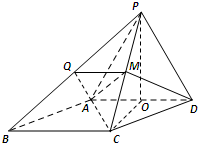 解:(Ⅰ)方法一:取AD中点O,连结OP,OC,AC,
解:(Ⅰ)方法一:取AD中点O,连结OP,OC,AC,
依题意可知:
△PAD,△ACD均为正三角形,
所以OC⊥AD,OP⊥AD,
又OC∩OP=O,OC?平面POC,OP?平面POC,
所以AD⊥平面POC,又PC?平面POC,
所以PC⊥AD.
方法二:连结AC、AM,依题意可知△PAC,△PCD均为边长为2正三角形,
又M为PC的中点,所以AM⊥PC,DM⊥PC,
又AM∩DM=M,AM?平面AMD,DM?平面AMD,
所以PC⊥平面AMD,
又AD?平面AMD,所以PC⊥AD;
(Ⅱ)当Q是PB中点时,平面MNQ∥PAD,
证明如下:
∵M、N是AC和PC的中点,∴MN∥AP,
∴MN∥平面PAD,
又∵Q、M是PB、PC的中点,∴QM∥BC∥AD,
∴QM∥平面PAD,
∵QM∩MN=M,
∴平面平面MNQ∥PAD;
(Ⅲ)点D到平面PAM的距离即点D到平面PAC的距离,
由(Ⅰ)可知PO⊥AD,又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
PO?平面PAD,所以PO⊥平面ABCD,
即PO为三棱锥P-ACD的高.
在RT△POC中,PO=OC=$\sqrt{3}$,PC=$\sqrt{6}$,
在△PAC中,PA=AC=2,PC=$\sqrt{6}$,
边PC上的高AM=$\sqrt{{PA}^{2}{-PM}^{2}}$=$\frac{\sqrt{10}}{2}$,
所以△PAC的面积S△PAC=$\frac{1}{2}$PC•AM=$\frac{1}{2}$×$\sqrt{6}$×$\frac{\sqrt{10}}{2}$=$\frac{\sqrt{15}}{2}$,
设点D到平面PAC的距离为h,
由VD-PAC=VP-ACD,S△ACD=$\frac{\sqrt{3}}{4}$×22=$\sqrt{3}$,
∴$\frac{1}{3}$×$\frac{\sqrt{15}}{2}$•h=$\frac{1}{3}$×$\sqrt{3}$×$\sqrt{3}$,
解得:h=$\frac{2\sqrt{15}}{5}$,所以点D到平面PAM的距离为$\frac{2\sqrt{15}}{5}$.
点评 本题考察了线面、面面垂直的性质即判定,考察线、面的距离,本题是一道中档题.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案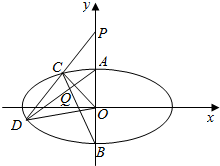 如图,椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,上、下顶点为A,B,点P(0,2)关于直线y=-x的对称点在椭圆M上,过点P的直线l与椭圆M相交于两个不同的点C,D(C在线段PD之间).
如图,椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,上、下顶点为A,B,点P(0,2)关于直线y=-x的对称点在椭圆M上,过点P的直线l与椭圆M相交于两个不同的点C,D(C在线段PD之间).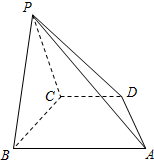 在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=90°,AB=PB=PC=BC=2CD,平面PBC⊥平面ABCD.
在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=90°,AB=PB=PC=BC=2CD,平面PBC⊥平面ABCD.
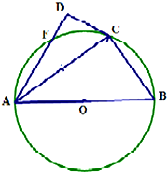 已知AB是⊙O的直径,F为圆上一点,∠BAF的角平分线与圆交于点C,过点C作圆的切线与直线AF相交于点D,若AB=6,∠DAB=$\frac{π}{3}$
已知AB是⊙O的直径,F为圆上一点,∠BAF的角平分线与圆交于点C,过点C作圆的切线与直线AF相交于点D,若AB=6,∠DAB=$\frac{π}{3}$