Question

已知方程x²+3nx+b_n=0的根为a_n、a_n+1，若a₁₀=-17，求b₅₁.

A.2024.     B.3015    C .5840    D.6970

Answer 1

C

解析:

：依题意有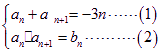，对任意n都成立，由，由（3）﹣（1）得：．由{a_n}的奇数项和偶数项分别组成-3为公差的等差数列，又有a₁₀=-17，所以有a₁=2，a₃=-1，a₅=-4，……，

  a₂=-5，a₄=-8，a₆=-11，……．又有b₅₁=a_51·a₅₂=5048.   选C. 

 (本题也可以通过求出通项求之)