题目内容
在直角坐标系中，△ABC的三个顶点坐标分别为A（3，4），B（0，0），C（c，0），若∠A为钝角，则c的取值范围为________．
分析：若∠A为钝角，则有cos∠A＜0且cos∠A≠-1．其中cos∠A＜0转化为
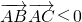，求出
，
，可得关于c的关系式，J即可得到答案．解答：由题意可知：
，
，所以，，不反向，若∠A为钝角，
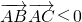，则-3c+16+9＜0，解得
，∴c的取值范围是
．故答案为：
．点评：本题容易忽视了两向量共线且反向时，此时的夹角为1800．两非零向量 的夹角为钝角的充要条件是
且 它们不平行． 
练习册系列答案
相关题目
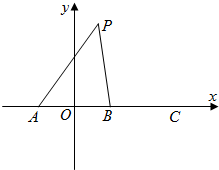如图，在直角坐标系中，A，B，C三点在x轴上，原点O和点B分别是线段AB和AC的中点，已知AO=m（m为常数），平面上的点P满足PA+PB=6m．
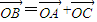（O是坐标原点），其中t∈（0，+∞）．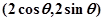
^
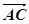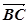,求
的值；