Question

【题目】已知一家公司生产某种品牌服装的年固定成本为10万元，每生产1千件需另投入2.7万元．设该公司一年内生产该品牌服装x千件并全部销售完，每千件的销售收入为R（x）万元，且R（x）= ．
（1）求年利润W（万元）关于年产量x（千件）的函数解析式；
（2）当年产量为多少千件时，该公司在这一品牌服装的生产中所获得的年利润最大，并求出最大值．

Answer 1

【答案】
（1）解：当0＜x≤10时，

W=xR（x）﹣（10+2.7x）=8.1x﹣ ﹣10，

当x＞10时，W=xR（x）﹣（10+2.7x）=98﹣ ﹣2.7x，

∴W= ．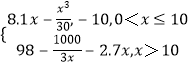

（2）解：①当0＜x≤10时，

由W′=8.1﹣ =0，得x=9，且当x∈（0，9）时，w′＞0，

当x∈（9，10）时，w′＜0．

∴当x=9时，W取最大值，且wmax=8.1×9﹣ ﹣10=38.6

x＞10时，W=98﹣（ ）≤98﹣2 =38，

当且仅当 =2.7x，即x= 时W取得最大值38．

综合①②知：当x=9时，W取得最大值38.6．故当年产量为9千件时，该公司在这一品牌服装的生产中所获的年利润最大．

【解析】（1）当0＜x≤10时，W=xR（x）﹣（10+2.7x）=8.1x﹣ ﹣10，当x＞10时，W=xR（x）﹣（10+2.7x）=98﹣ ﹣2.7x，由此能求出年利润W（万元）关于该特许商品x（千件）的函数解析式．（2）当0＜x≤10时，由W′=8.1﹣ =0，得x=9，推导出当x=9时，W取最大值，且wmax=38.6；当x＞10时，W≤38．由此得到当年产量为9千件时，该公司在该特许商品生产中获利最大．