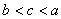题目内容
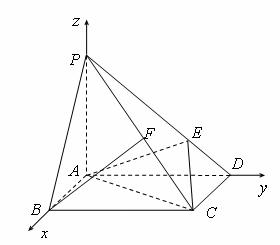
如图,在底面是正方形的四棱锥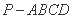 中,
中,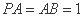 ,
,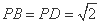 ,点
,点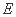 在
在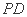 上,且
上,且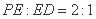 .
.
(Ⅰ)求证: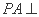 平面
平面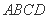 ;
;
(Ⅱ)求二面角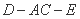 的余弦值;
的余弦值;
(Ⅲ)在棱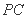 上是否存在一点
上是否存在一点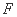 ,使得
,使得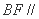 平面
平面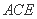 .
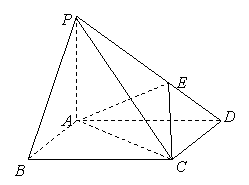
.
解:(Ⅰ)正方形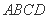 边长为1,
边长为1,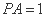 ,
,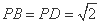 ,
,
所以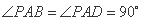 ,即
,即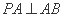 ,
,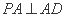 ,
,
因为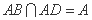 ,
,
所以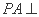 平面
平面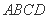 . ………………4分
. ………………4分
(Ⅱ)如图,以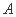 为坐标原点,直线
为坐标原点,直线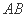 ,
,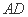 ,
,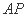 分别为
分别为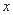 轴,
轴,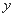 轴,
轴,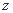 轴,建立空间直角坐标系,则
轴,建立空间直角坐标系,则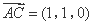 ,
,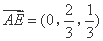 .
.
 由(Ⅰ)知
由(Ⅰ)知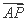 为平面
为平面 的法向量,
的法向量,
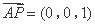 ,
,
设平面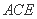 的法向量为
的法向量为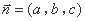 ,
,
由 ,
,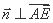 ,
,
得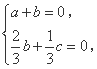
令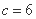 ,则
,则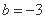 ,
,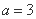 ,
,
所以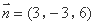 ,
,
所以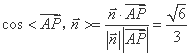 ,
,
即所求二面角的余弦值为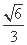 .
.
(Ⅲ)设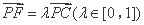 ,则
,则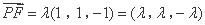 ,
,
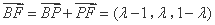 ,
,
若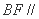 平面
平面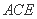 ,则
,则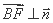 ,即
,即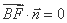 ,
,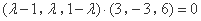 ,
,
解得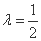 ,
,
所以存在满足题意的点,
当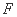 是棱
是棱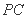 的中点时,
的中点时,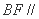 平面
平面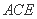 .
.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
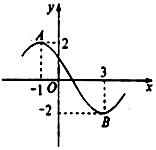
 (
( ,
,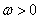 ,
, )的部分图象,那么
)的部分图象,那么 ( )
( ) B.
B. C.
C. D.
D.
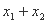 =6,那么
=6,那么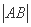 = ( )
= ( ) 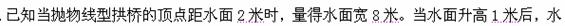

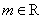 ,则“
,则“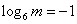 ”是“直线
”是“直线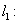
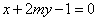 与
与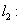
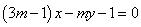 平行”的( )
平行”的( ) 为原点,双曲线
为原点,双曲线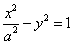 (
(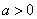 )上有一点
)上有一点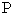 ,过
,过 ,
,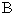 ,平行四边形
,平行四边形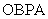 的面积为
的面积为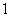 ,则双曲线的离心率为( )
,则双曲线的离心率为( )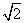 B.
B.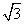 C.
C.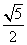 D.
D.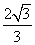
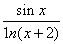 的图象可能是
的图象可能是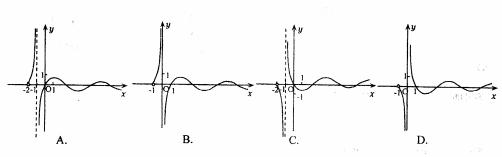
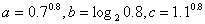 ,则
,则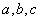 的大小关系是( )
的大小关系是( ) B.
B. C.
C.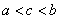 D.
D.