题目内容
(10分)盒中共有9个球,其中有4个红球,3个黄球和2个绿球,这些球除颜色外完全相同.
(1)从盒中一次随机抽出2个球,求取出的2个球的颜色相同的概率;
(2)从盒中一次随机抽出4个球,其中红球、黄球、绿球的个数分别为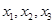 ,随机变量
,随机变量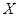 表示
表示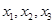 的最大数,求
的最大数,求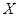 的概率分布和数学期望
的概率分布和数学期望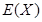 .
.
(1) ;(2)
;(2) .
.
解析试题分析:(1)从9个球中抽2个球共有 种方法,而两个球同色,可能同为红,同为黄或同为绿,方法为
种方法,而两个球同色,可能同为红,同为黄或同为绿,方法为 ,概率为
,概率为 ;(2)首先抽4个球中,红、黄、绿色球的个数至少有一个不小于2,因此
;(2)首先抽4个球中,红、黄、绿色球的个数至少有一个不小于2,因此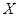 的可能值为
的可能值为 ,
, ,说明抽出的4个球都是红球,
,说明抽出的4个球都是红球, ,说明抽出的4个球中有3个红球、1个其他色或者3个黄球、1个其他色,
,说明抽出的4个球中有3个红球、1个其他色或者3个黄球、1个其他色, 说明4个球中2个红球、其他两色各1个,或2个黄球、其他两色各1个,或2个绿球、其他两色各1个,当然求
说明4个球中2个红球、其他两色各1个,或2个黄球、其他两色各1个,或2个绿球、其他两色各1个,当然求 时,可用
时,可用 来求.
来求.
试题解析:
(1)由题意 ;
;
(2)随机变量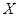 的取值可能为
的取值可能为 ,
, ,
, ,
, ,
,
所以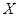 的分布列为
的分布列为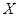
2
3
4



 .
.
【考点】排列与组合,离散型随机变量的分布列与均值(数学期望).

练习册系列答案
相关题目
 6的二项展开式中,常数项等于 _________ .
6的二项展开式中,常数项等于 _________ .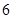 名同学.
名同学.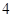 人参加班级
人参加班级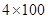 接力比赛,则同学丙不跑第一棒的安排方法有多少种?
接力比赛,则同学丙不跑第一棒的安排方法有多少种? 的展开式中,第6项
的展开式中,第6项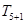 为常数项.
为常数项.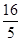 x2+
x2+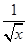 )5的展开式的常数项,而(a2+1)n的展开式的二项式系数最大的项等于54,求a的值.
)5的展开式的常数项,而(a2+1)n的展开式的二项式系数最大的项等于54,求a的值. -
- )n的展开式中,第五项与第三项的二项式系数之比为14∶3,求展开式中的常数项.
)n的展开式中,第五项与第三项的二项式系数之比为14∶3,求展开式中的常数项.