在正方体ABCD-A1B1C1D1中.E.F分别是C1D.BC的中点.则直线A1B与直线EF的位置关系是( )A．相交B．平行C．异面D．无法确定题目和参考答案——青夏教育精英家教网—

题目内容

5．在正方体ABCD-A₁B₁C₁D₁中，E，F分别是C₁D，BC的中点，则直线A₁B与直线EF的位置关系是（　　）

A．

相交

B．

平行

C．

异面

D．

无法确定

分析连结CD₁，则直线A₁B与直线EF均在平面A₁BCD₁上，由A₁B∥CD₁，EF与CD₁相交可判断结论．

解答解：连结CD₁，∵BC$\stackrel{∥}{=}$A₁D₁，∴四边形A₁BCD₁是平行四边形，
∵A₁B?平面A₁BCD₁，EF?平面A₁BCD₁，∴A₁B与EF共面，
∵A₁B∥CD₁，EF与CD₁相交，∴直线A₁B与直线EF相交．
故选：A．

点评本题考查了直线的位置关系判断，属于基础题．

练习册系列答案

11．正项数列a₁，a₂，…，a_m（m≥4，m∈N^*）满足：a₁，a₂，a₃，…，a_k-1，a_k（k＜m，k∈N^*）是公差为d的等差数列，a₁，a_m，a_m-1，…，a_k+1，a_k是公比为2的等比数列．
（1）若a₁=d=2，k=8，求数列a₁，a₂，…，a_m的所有项的和S_m；
（2）若a₁=d=2，m＜2016，求m的最大值；
（3）是否存在正整数k，满足a₁+a₂+…+a_k-1+a_k=3（a_k+1+a_k+2+…+a_m-1+a_m）？若存在，求出k值；若不存在，请说明理由．

13．若动点M（x，y）始终满足关系式$\sqrt{{x}^{2}+（y+2）^{2}}$+$\sqrt{{x}^{2}+（y-2）^{2}}$=8，则动点N的轨迹方程为（　　）

A．

$\frac{x^2}{16}+\frac{y^2}{12}$=1

B．

$\frac{x^2}{12}+\frac{y^2}{16}$=1

C．

$\frac{x^2}{12}-\frac{y^2}{16}$=1

D．

$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{12}$=1

20．

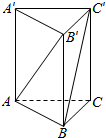如图，在正三棱柱ABC-A′B′C′中，若AA′=2AB，则异面直线AB′与BC′所成角的余弦值为（　　）

10．已知函数$f（x）=sin（2x-\frac{π}{6}）$．
（I）求函数f（x）的最小正周期；
（Ⅱ）求函数f（x）的单调递增区间；
（Ⅲ）当$x∈[{0，\frac{2π}{3}}]$时，求函数f（x）的最小值，并求出使y=f（x）取得最小值时相应的x值．

17．抛物线y²=2px（p＞0）与直线y=x+1相切，A（x₁，y₁），B（x₂，y₂）（x₁≠x₂）是抛物线上两个动点，F为抛物线的焦点，且|AF|+|BF|=8．
（Ⅰ）求p的值；
（Ⅱ）线段AB的垂直平分线l与x轴的交点是否为定点，若是，求出交点坐标，若不是，说明理由；
（Ⅲ）求直线l的斜率的取值范围．

14．

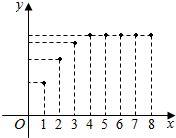甲工厂八年来某种产品年产量与时间（单位：年）的函数关系如图所示．现有下列四种说法：
①前三年该产品产量增长速度越来越快；
②前三年该产品产量增长速度越来越慢；
③第三年后该产品停止生产；
④第三年后该产品年产量保持不变．
其中说法正确的是（　　）

15．设向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=3，$\overrightarrow{a}$•$\overrightarrow{b}$=-5，且|$\overrightarrow{a}$+2$\overrightarrow{b}$|=1，则|$\overrightarrow{b}$|等于（　　）

试题分类