题目内容
若函数f(x)=x2+(k-2)x+2k-1=0的两个零点中,一个在0和1之间,另一个在1和2之间,求k的取值范围.
思路分析:本题考查一元二次方程根的分布.画出函数图像,通过数形结合的思想来解.
解:如下图所示,函数f(x)=x2+(k-2)x+2k-1的图像开口向上,零点x1∈(0,1),x2∈(1,2).
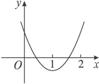
结合图像得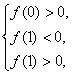 即
即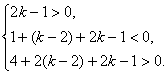 解得
解得![]() <k<
<k<![]() ,
,
即k的取值范围是(![]() ,
,![]() ).
).
绿色通道:对于二次函数零点的分布问题,画出图像后,根据二次函数相应特征列不等式(组)求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目