题目内容
(1)已知sin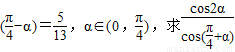 的值.
的值.(2)已知tanα=-
 ,求
,求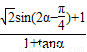 的值.
的值.
【答案】分析:(1)根据同角三角函数的基本关系求出cos(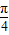 -α)的值,进而可知sin(
-α)的值,进而可知sin(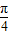 +α)的值,然后由利用二倍角公式、诱导公式化简所求的式子为2sin(
+α)的值,然后由利用二倍角公式、诱导公式化简所求的式子为2sin(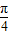 +α),即可得出结果.
+α),即可得出结果.
(2)利用二倍角公式以及同角三角函数的基本关系化简得2sinαcosα,然后分子分母同除以sin2α+cos2α,然后将值代入即可.
解答:解:(1)∵sin(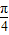 -α)=
-α)=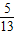 ,α∈(0,
,α∈(0,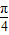 )
)
∴cos(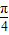 -α)=
-α)=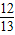
sin(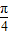 +α)=
+α)=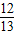
∴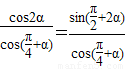 =2sin(
=2sin(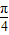 +α)=
+α)=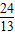
(2)∵tanα=- ,
,
∴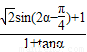 =
=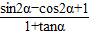 =
=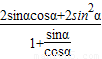 =2sinαcosα=
=2sinαcosα=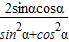 =
=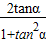 =-
=-
点评:此题考查了二倍角公式、两角和与差公式以及同角三角函数的基本关系,熟练掌握公式是解题的关键,属于中档题.
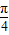 -α)的值,进而可知sin(
-α)的值,进而可知sin(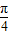 +α)的值,然后由利用二倍角公式、诱导公式化简所求的式子为2sin(
+α)的值,然后由利用二倍角公式、诱导公式化简所求的式子为2sin(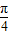 +α),即可得出结果.
+α),即可得出结果.(2)利用二倍角公式以及同角三角函数的基本关系化简得2sinαcosα,然后分子分母同除以sin2α+cos2α,然后将值代入即可.
解答:解:(1)∵sin(
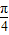 -α)=
-α)=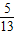 ,α∈(0,
,α∈(0,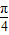 )
)∴cos(
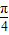 -α)=
-α)=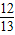
sin(
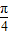 +α)=
+α)=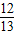
∴
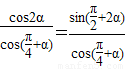 =2sin(
=2sin(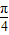 +α)=
+α)=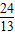
(2)∵tanα=-
 ,
,∴
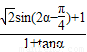 =
=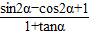 =
=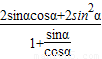 =2sinαcosα=
=2sinαcosα=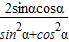 =
=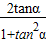 =-
=-
点评:此题考查了二倍角公式、两角和与差公式以及同角三角函数的基本关系,熟练掌握公式是解题的关键,属于中档题.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
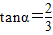 ,
,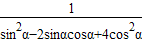 的值.
的值.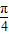 <α<
<α<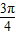 ,0<β<
,0<β<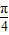 ,且cos(
,且cos(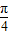 -α)=
-α)= ,sin(
,sin(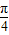 +β)=
+β)=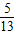 ,求sin(α+β)的值.
,求sin(α+β)的值.