题目内容
【题目】如图,已知圆![]() :
: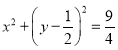 经过椭圆
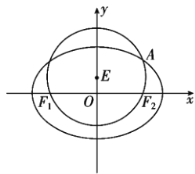
经过椭圆![]() :
:![]() (
(![]() )的左右焦点
)的左右焦点![]() ,
,![]() ,与椭圆
,与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() ,
,![]() ,
,![]() 三点共线.
三点共线.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设与直线![]() (
(![]() 为原点)平行的直线
为原点)平行的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点.当
两点.当![]() 的面积取到最大值时,求直线
的面积取到最大值时,求直线![]() 的方程.
的方程.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
试题分析:(Ⅰ)由![]() ,
,![]() ,
,![]() 三点共线可知
三点共线可知![]() 为圆
为圆![]() 的直径,从而可得
的直径,从而可得![]() ,在圆方程中令
,在圆方程中令![]() 求出
求出![]() 即
即![]() ,由勾股定理可求得
,由勾股定理可求得![]() ,由椭圆定义求出
,由椭圆定义求出![]() 的值即可;(Ⅱ)设直线
的值即可;(Ⅱ)设直线![]() 的方程为
的方程为![]() ,联立方程组,由弦长公式求出
,联立方程组,由弦长公式求出![]() ,由点到直线的距离公式求出
,由点到直线的距离公式求出![]() 到直线
到直线![]() 的距离
的距离![]() ,求出三角形面积表达式
,求出三角形面积表达式![]() ,由基本不等式求最值及取得最值时
,由基本不等式求最值及取得最值时![]() 的值即可.
的值即可.
试题解析:(Ⅰ)![]() ,
,![]() ,
,![]() 三点共线,
三点共线,![]() 为圆
为圆![]() 的直径,且
的直径,且![]() ,
,
![]() .
.
由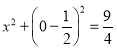 ,
,
得![]() ,
,
![]() …(2分)
…(2分)
![]() ,
,![]()
![]() ,
,![]() .(3分)
.(3分)
![]() ,
,![]() ,………(4分)
,………(4分)
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .…(5分)
.…(5分)
(Ⅱ)由(Ⅰ)知,点![]() 的坐标为
的坐标为![]() ,
,
![]() 直线
直线![]() 的斜率为
的斜率为![]() (6分)
(6分)
故设直线![]() 的方程为
的方程为![]() ,
,
联立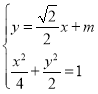 得,
得,![]() …………(7分)
…………(7分)
设![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() .……(8分)
.……(8分)
又![]()
![]() ……(9分)
……(9分)
![]() 点
点![]() 到直线
到直线![]() 的距离
的距离![]() (10分)
(10分)
![]()
![]() ,
,
当且仅当![]() ,即
,即![]() 时等号成立,
时等号成立,
此时直线![]() 的方程为
的方程为![]() .…………(12分)
.…………(12分)

练习册系列答案
相关题目