题目内容
正方体ABCD-A'B'C'D'中,棱长为2,则异面直线A1B1与BC1的距离是________.

分析:连接B1C、BC1,交于O,可以证明A1B1⊥B1C.又B1C⊥BC1 所以B1O是A1B1与BC1的公垂线段,B1O的长度即为异面直线A1B1与BC1的距离.
解答:
 连接B1C,BC1,交于O,由正方体的性质可知,A1B1⊥面BCC1B1,B1C?面BCC1B1∴,A1B1⊥B1C.又B1C⊥BC1,∴B1O是A1B1与BC1的公垂线段,B1O的长度即为异面直线A1B1与BC1的距离,∵正方体ABCD-A'B'C'D'中,棱长为2∴B1O=
连接B1C,BC1,交于O,由正方体的性质可知,A1B1⊥面BCC1B1,B1C?面BCC1B1∴,A1B1⊥B1C.又B1C⊥BC1,∴B1O是A1B1与BC1的公垂线段,B1O的长度即为异面直线A1B1与BC1的距离,∵正方体ABCD-A'B'C'D'中,棱长为2∴B1O= .
.故答案为:
 .
.点评:本题考查异面直线的距离,利用定义找出异面直线的公垂线段是关键. 考查考查空间想象、转化、计算的能力.

练习册系列答案
相关题目
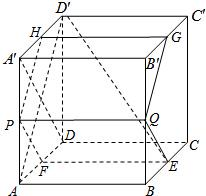 如图,在棱长为1的正方体ABCD-A′B′C′D′中,AP=BQ=b(0<b<1),截面PQEF∥A′D,截面PQGH∥AD′.
如图,在棱长为1的正方体ABCD-A′B′C′D′中,AP=BQ=b(0<b<1),截面PQEF∥A′D,截面PQGH∥AD′.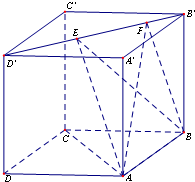 如图,正方体ABCD-A′B′C′D′的棱长为1,线段B′D′上有两个动点E,F且
如图,正方体ABCD-A′B′C′D′的棱长为1,线段B′D′上有两个动点E,F且 (2011•蓝山县模拟)如图,在正方体ABCD-A′B′C′D′中,异面直线BD与B′C所成角为
(2011•蓝山县模拟)如图,在正方体ABCD-A′B′C′D′中,异面直线BD与B′C所成角为