题目内容
已知椭圆C: (a>0,b>0)的离心率为
(a>0,b>0)的离心率为 ,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+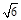 =0相切.又设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连结PB交椭圆C于另一点E.
=0相切.又设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连结PB交椭圆C于另一点E.
(Ⅰ)求椭圆C的方程;
(Ⅱ)证明:直线AE与x轴相交于定点Q;
(III)求 的取值范围.
的取值范围.
【答案】
解:(1)由题意知 ,
,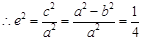 ,即
,即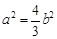 ,
,
又 ,
,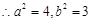 ,故椭圆
,故椭圆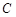 的方程为
的方程为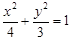 3分
3分
(2)由题意知直线 的斜率存在,设直线
的斜率存在,设直线 的方程为
的方程为 ,
,
由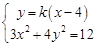 ,德
,德 ①
①
设点 ,得
,得 5分
5分
 ,即
,即 , 6分
, 6分
又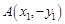 ,直线
,直线 的方程为
的方程为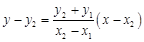 , 7分
, 7分
令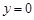 ,得
,得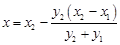 ,
,
将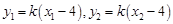 代入整理得
代入整理得 ② 9分
② 9分
由①得,代入②整理得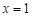 ,
,
所以直线 与
与 轴相交于定点
轴相交于定点 ; 11分
; 11分
(3)由(2)有
 15分
15分
【解析】略

练习册系列答案
相关题目
 +
+ =1(a>b>0),直线y=x+
=1(a>b>0),直线y=x+ 与以原点为圆心,以椭圆C的短半轴长为半径
与以原点为圆心,以椭圆C的短半轴长为半径 ,0)求实数k的取值范围。
,0)求实数k的取值范围。 +
+ =1(a>b>0),直线y=x+
=1(a>b>0),直线y=x+ 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同两点A,B且线段AB的垂直平分线过定点C(
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同两点A,B且线段AB的垂直平分线过定点C( ,0)求实数k的取值范围。
,0)求实数k的取值范围。 (a>b>0),直线y=x+
(a>b>0),直线y=x+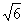 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1、F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1、F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。 ,0),求实数k的取值范围。
,0),求实数k的取值范围。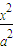 +
+ (a>b>0)的焦距为4,且过点P(
(a>b>0)的焦距为4,且过点P( ,
, ).
). ),连接AE,过点A作AE的垂线交x轴于点D.点G是点D关于y轴的对称点,作直线QG,问这样作出的直线QG是否与椭圆C一定有唯一的公共点?并说明理由.
),连接AE,过点A作AE的垂线交x轴于点D.点G是点D关于y轴的对称点,作直线QG,问这样作出的直线QG是否与椭圆C一定有唯一的公共点?并说明理由. (a>b>0),直线l过点A(a,0)和
(a>b>0),直线l过点A(a,0)和