题目内容
已知sinα＋cosα＝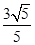
，α∈(0，
)，sin(β－)＝
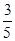，β∈(，
)．
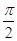(1) 求sin2α和tan2α的值；
(2) 求cos(α＋2β)的值．
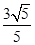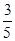，α∈(0，)，sin(β－)＝，β∈(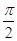，)．(1) 求sin2α和tan2α的值；
(2) 求cos(α＋2β)的值．
(1)由题意得(sinα＋cosα)2＝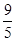
，即1＋sin2α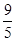＝，∴sin2α＝
.
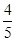又2α∈(0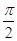，)，∴cos2α＝
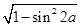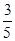＝，∴tan2α＝
＝
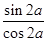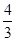. ……4分
(2)∵β∈(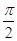，)，β－∈(0，)，∴cos(β－)＝，
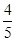于是sin2(β－)＝2sin(β－)cos(β－)＝
.
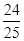又sin2(β－)＝－cos2β，∴cos2β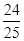＝－.又2β∈(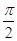，π)，∴sin2β＝
.
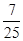又cos2α＝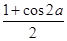
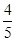＝，∴cosα＝
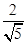，sinα＝
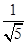(α∈(0，))．
∴cos(α＋2β)＝cosαcos2β－sinαsin2β＝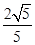
×(－)－
×＝－
.
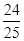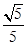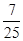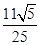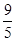，即1＋sin2α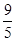＝，∴sin2α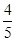＝.又2α∈(0，
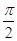)，∴cos2α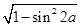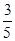＝＝，∴tan2α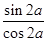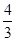＝＝. ……4分(2)∵β∈(
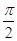，)，β－∈(0，)，∴cos(β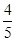－)＝，于是sin2(β－
)＝2sin(β－)cos(β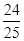－)＝.又sin2(β－
)＝－cos2β，∴cos2β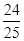＝－.又2β∈(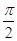，π)，∴sin2β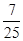＝.又cos2α＝
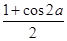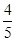＝，∴cosα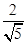＝，sinα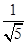＝(α∈(0，))．∴cos(α＋2β)＝cosαcos2β－sinαsin2β＝
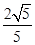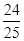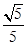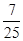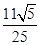×(－)－×＝－.略
练习册系列答案
阅读快车系列答案
相关题目
（
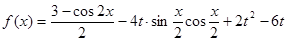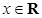），其中
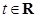，将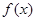
的最小值记为
．
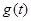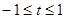时，要使关于
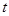的方程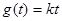
有且仅有一个实根，求实数
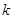的取值范围．
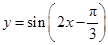在区间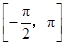
的简图是（ ）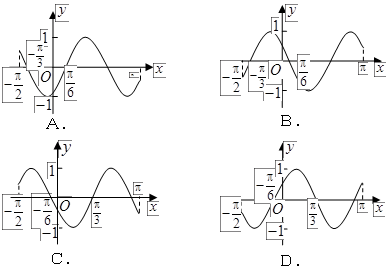
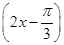＋cos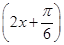
，有下列命题：
；
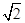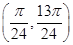上单调递减；
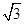cosωx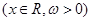
满足f(α)＝－2，f(β)＝0，且｜α－β｜的最小值为
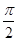，则函数f(x)的单调增区间为_____________
图像如图所示,则
的值等于（▲）
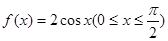的值域是 。
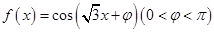。若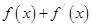
是奇函数，则
_________。
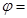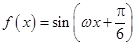
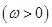的相邻两个零点之间的距离为
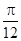，则
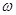的值为