题目内容
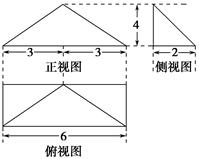
下图是一几何体的直观图、主视图、俯视图、左视图.

(1)若 为
为 的中点,求证:
的中点,求证:
 面
面 ;
;
(2)证明 面
面 .
.
(3)求该几何体的体积.

(1)若
 为
为 的中点,求证:
的中点,求证:
 面
面 ;
;(2)证明
 面
面 .
.(3)求该几何体的体积.
(1)详见解析;(2)详见解析;(3)

试题分析:由三视图可知底面是边长为4的正方形,
 ,
, ,
, ∥
∥ ,且
,且 。(1)根据等腰三角形中线即为高线可证得
。(1)根据等腰三角形中线即为高线可证得 ,根据
,根据 ,且
,且 为正方形可证得
为正方形可证得 ,即可证得
,即可证得 ,根据线面垂直的判定定理可得
,根据线面垂直的判定定理可得 。(2)取
。(2)取 的中点
的中点 ,
,  与
与 的交点为
的交点为 ,可证得四边形
,可证得四边形 平行四边形,即可证得
平行四边形,即可证得 ∥
∥ ,根据线面平行的定义即可证得
,根据线面平行的定义即可证得 面
面 。(3)用分割法求体积,即将此几何体分割成以
。(3)用分割法求体积,即将此几何体分割成以 为顶点的一个四棱锥和一个三棱锥。
为顶点的一个四棱锥和一个三棱锥。试题解析:解:(1)由几何体的三视图可知,底面
 是边长为4的正方形,
是边长为4的正方形,而且
 ,
, ∥
∥ ,
, ,
, .
.取
 的中点
的中点 ,如图所示.
,如图所示.∵
 ,∴
,∴ ,
,又∵
 ,∴
,∴ 面
面 ,
,∴
 .又
.又 ,
,∴
 面
面 . 5分
. 5分(2)如图

取
 的中点
的中点 ,
,  与
与 的交点为
的交点为 ,
,连结
 、
、 ,如图所示.
,如图所示.∴
 ,
, ∥
∥ ,∴
,∴ ,
, ∥
∥ ,
,∴四边形
 为平行四边形,
为平行四边形,∴
 ∥
∥ ,又
,又
 面
面 , ∴
, ∴ ∥面
∥面 ,
,∴
 面
面 . 9分
. 9分(3)
 . 13分
. 13分
练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
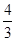 πr3,观察发现V′=S.则由四维空间中“超球”的三维测度V=8πr3,猜想其四维测度W=________.
πr3,观察发现V′=S.则由四维空间中“超球”的三维测度V=8πr3,猜想其四维测度W=________.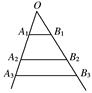
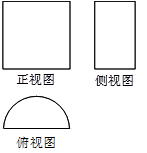
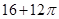




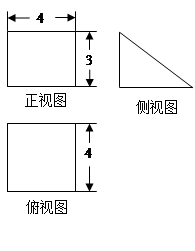





 ,则这个三棱柱的体积为________.
,则这个三棱柱的体积为________.