题目内容
如图所示,圆O
的直径AB=10,弦DE⊥AB于点H,BH=2,延长ED到P,过P作圆O的切线,切点为C.
(1)求DE的长.
(2)若PC=2
,求PD的长.
解析】(1)因为AB为圆O的直径,AB⊥DE,
所以DH=HE,AD⊥DB.
由直角三角形的射影定理得
DH2=AH·BH=(10-2)×2=16,
所以DH=4,DE=8.
(2)因为PC切圆O于点C,
由切割线定理得PC2=PD·PE,
即(2)2=PD·(PD+8),得PD=2.
练习册系列答案
相关题目
5、如图所示，圆O的直径AB=6，C为圆周上一点，BC=3过C作圆的切线l，过A作l的垂线AD，垂足为D，则∠DAC=（ ）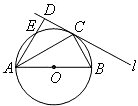
如图所示，圆O的直径AB=6，C为圆周上一点，BC=3，过C作圆的切线l，则点A到直线l的距离AD为
15、如图所示，圆O的直径AB=6，C为圆周上一点，BC=3过C作圆的切线l，过A作l的垂线AD，垂足为D，则∠DAC=
（2013•营口二模）（几何证明选讲选做题）如图所示，圆O的直径AB=6，C为圆周上一点，BC=3．过C作圆的切线l，过A作l的垂线AD，AD分别与直线l、圆交于点D，E，则∠DAC=
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）